Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
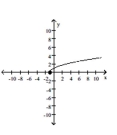
The graph of a function is given. Decide whether it is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (38)
(38)
Answer the question about the given function.
-Given the function , list the -intercept, if there is one, of the graph of .
(Multiple Choice)
4.9/5  (31)
(31)
The graph of a function f is given. Use the graph to answer the question.
-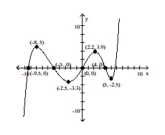 Find the numbers, if any, at which f has a local minimum. What are the local maxima? A) f has a local minimum at and 5 ; the local minimum at is ; the local minimum at 5 is
B) f has a local maximum at and 5 ; the local maximum at is ; the local maximum at 5 is
C) f has a local minimum at and ; the local minimum at is ; the local minimum at is 5
D) f has a local maximum at and ; the local maximum at is ; the local maximum at is 5
Find the numbers, if any, at which f has a local minimum. What are the local maxima? A) f has a local minimum at and 5 ; the local minimum at is ; the local minimum at 5 is
B) f has a local maximum at and 5 ; the local maximum at is ; the local maximum at 5 is
C) f has a local minimum at and ; the local minimum at is ; the local minimum at is 5
D) f has a local maximum at and ; the local maximum at is ; the local maximum at is 5
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-Two boats leave a dock at the same time. One boat is headed directly east at a constant speed of 35 knots
(nautical miles per hour), and the other is headed directly south at a constant speed of 22 knots. Express the
distance d between the boats as a function of the time t.
(Essay)
4.7/5  (27)
(27)
Find and simplify the difference quotient of f, , for the function.
- A)
function
domain:
range:
intercepts:
symmetry: -axis, -axis
B)
function
domain:
range:
intercepts:
symmetry: -axis, -axis, origin
C)
function
domain:
range:
intercepts:
symmetry: origin
D)not a function
A)
function
domain:
range:
intercepts:
symmetry: -axis, -axis
B)
function
domain:
range:
intercepts:
symmetry: -axis, -axis, origin
C)
function
domain:
range:
intercepts:
symmetry: origin
D)not a function
(Multiple Choice)
4.8/5  (36)
(36)
Determine whether the equation defines y as a function of x.
-
(Multiple Choice)
4.8/5  (37)
(37)
The graph of a function f is given. Use the graph to answer the question.
-For what numbers x is f(x) = 0? 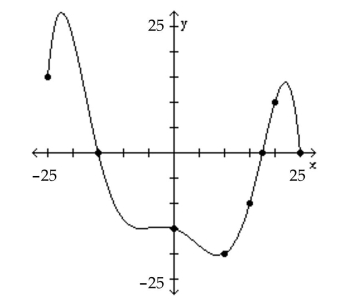
(Multiple Choice)
4.7/5  (29)
(29)
Solve the problem.
-A rectangular sign is being designed so that the length of its base, in feet, is 10 feet less than 4 times the height, h. Express the area of the sign as a function of h. A)
B)
C)
D)
(Multiple Choice)
4.9/5  (35)
(35)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (45)
(45)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.8/5  (37)
(37)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
5.0/5  (33)
(33)
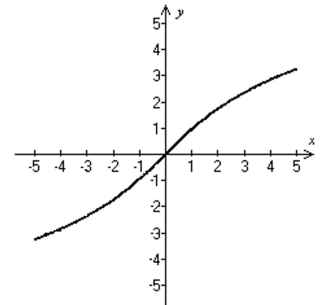
Use the graph to find the intervals on which it is increasing, decreasing, or constant.
-
(Multiple Choice)
4.7/5  (33)
(33)
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
4.9/5  (37)
(37)
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
4.8/5  (34)
(34)
Match the function with the graph that best describes the situation.
-The concentration C (arbitrary units) of a certain drug in a patient's bloodstream can be modeled using where t is the number of hours since a 500 milligram oral dose was administered. Using the TABLE feature of a graphing utility, find the time at which the concentration of the drug is greatest. Round
To the nearest tenth of an hour.
(Multiple Choice)
4.8/5  (34)
(34)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.9/5  (41)
(41)
Showing 121 - 140 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)