Exam 1: Functions and Their Graphs
Exam 1: Functions and Their Graphs301 Questions
Exam 2: Linear and Quadratic Functions301 Questions
Exam 3: Polynomial and Rational Functions350 Questions
Exam 4: Exponential and Logarithmic Functions518 Questions
Exam 5: Trigonometric Functions366 Questions
Exam 6: Analytic Trigonometry402 Questions
Exam 7: Applications of Trigonometric Functions103 Questions
Exam 8: Polar Coordinates; Vectors270 Questions
Exam 9: Analytic Geometry197 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability108 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Review228 Questions
Select questions type
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
4.8/5  (37)
(37)
Find an equation of the secant line containing (1, f(1)) and (2, f(2)).
-
(Multiple Choice)
4.8/5  (30)
(30)
Write the word or phrase that best completes each statement or answers the question.
-A gas company has the following rate schedule for natural gas usage in single-family residences:
Monthly service charge \ 8.80 Per therm service charge 1st 25 therms \ 0.6686 / therm Over 25 therms \ 0.85870/ therm
What is the charge for using 25 therms in one month?
What is the charge for using 45 therms in one month?
Construct a function that gives the monthly charge C for x therms of gas.
(Essay)
4.9/5  (30)
(30)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.9/5  (27)
(27)
Choose the one alternative that best completes the statement or answers the question.
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
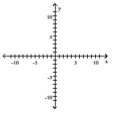 A)
A)
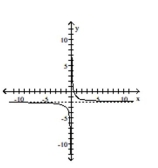 B)
B)
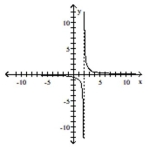 C)
C)
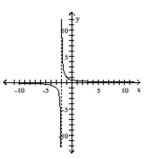 D)
D)
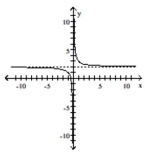
(Multiple Choice)
4.8/5  (31)
(31)
Graph the function by starting with the graph of the basic function and then using the techniques of shifting,
compressing, stretching, and/or reflecting.
-
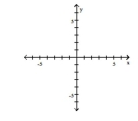 A)
A)
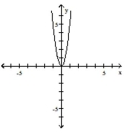 B)
B)
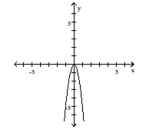 C)
C)
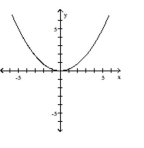 D)
D)
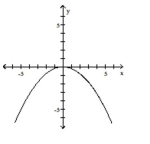
(Multiple Choice)
4.8/5  (38)
(38)
For the given functions f and g, find the requested function and state its domain.
-
Find .
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-If a rock falls from a height of 70 meters on Earth, the height H (in meters) after x seconds is approximately When does the rock strike the ground? Round to the nearest hundredth, if necessary.
(Multiple Choice)
4.8/5  (30)
(30)
Find and simplify the difference quotient of f, , for the function.
-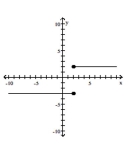 A)
function domain: all real numbers range: all real numbers intercept: (0,-3) symmetry: none
B)
function domain: \{x\midx=2 or x=-3\} range: all real numbers intercept: (-3,0) symmetry: x -axis
C)
function
domain: all real numbers
range: or
intercept:
symmetry: none
D)
not a function
A)
function domain: all real numbers range: all real numbers intercept: (0,-3) symmetry: none
B)
function domain: \{x\midx=2 or x=-3\} range: all real numbers intercept: (-3,0) symmetry: x -axis
C)
function
domain: all real numbers
range: or
intercept:
symmetry: none
D)
not a function
(Multiple Choice)
4.8/5  (37)
(37)
If y varies directly as x, find a linear function which relates them.
- when
(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-If an object weighs m pounds at sea level, then its weight W (in pounds) at a height of h miles above sea level is given approximately How much will a man who weighs 165 pounds at sea level
Weigh on the top of a mountain which is 14,494 feet above sea level? Round to the nearest hundredth of a
Pound, if necessary.
(Multiple Choice)
4.9/5  (27)
(27)
Based on the graph, find the range of y = f(x).
-
![Based on the graph, find the range of y = f(x). - f ( x ) = \left\{ \begin{array} { l l } 4 & \text { if } - 6 \leq x < - 2 \\ | x | & \text { if } - 2 \leq x < 5 \\ \sqrt [ 3 ] { x } & \text { if } 5 \leq x \leq 12 \end{array} \right. A) [ 0,5 ) B) [ 0,5 ] C) [ 0 , \infty ) D) [ 0 , \sqrt [ 3 ] { 12 } ]](https://storage.examlex.com/TB7697/11ed7e30_fc78_ab75_b337_cd7345d42163_TB7697_11.jpg) A)
B)
C)
D)
A)
B)
C)
D)
(Multiple Choice)
4.7/5  (36)
(36)
The graph of a function is given. Determine whether the function is increasing, decreasing, or constant on the given
interval.
-
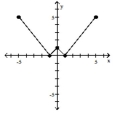
(Multiple Choice)
4.9/5  (30)
(30)
Determine algebraically whether the function is even, odd, or neither.
-
(Multiple Choice)
4.8/5  (39)
(39)
Find the average rate of change for the function between the given values.
-
(Multiple Choice)
4.9/5  (32)
(32)
Based on the graph, find the range of y = f(x).
-
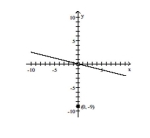 A) or
B)
C)
D) or or
A) or
B)
C)
D) or or
(Multiple Choice)
4.7/5  (35)
(35)
Match the graph to the function listed whose graph most resembles the one given.
-
(Multiple Choice)
4.8/5  (29)
(29)
Find the average rate of change for the function between the given values.
- from 0 to 2
(Multiple Choice)
4.8/5  (29)
(29)
Showing 141 - 160 of 301
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)