Exam 9: Introduction to Hypothesis Testing

In a hypothesis test, increasing the sample size will generally result in a smaller chance of making a Type I error since sampling error is likely to be reduced.

When testing a two-tailed hypothesis using a significance level of 0.05, a sample size of n = 16, and with the population standard deviation unknown, which of the following is true?

A contract calls for the mean diameter of a cylinder to be 1.50 inches. As a quality check, each day a random sample of n = 36 cylinders is selected and the diameters are measured. Assuming that the population standard deviation is thought to be 0.10 inch and that the test will be conducted using an alpha equal to 0.025, what would the probability of a Type II error be?

Lube-Tech is a major chain whose primary business is performing lube and oil changes for passenger vehicles. The national operations manager has stated in an industry newsletter that the mean number of miles between oil changes for all passenger cars exceeds 4,200 miles. To test this, an industry group has selected a random sample of 100 vehicles that have come into a lube shop and determined the number of miles since the last oil change and lube. The sample mean was 4,278 and the sample standard deviation was 780 miles. Based on this information, the test statistic is approximately t = 1.000.

The probability of a Type II error decreases as the "true" population value gets farther from the hypothesized population value, given that everything else is held constant.

For the following hypothesis test:

Which of the following will be helpful if the decision maker wishes to reduce the chance of making a Type II error?

When a battery company claims that their batteries last longer than 100 hours and a consumer group wants to test this claim, the hypotheses should be: H0 : μ ≤ 100 HA : μ > 100

You are given the following null and alternative hypotheses: 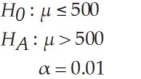Calculate the probability of committing a Type II error when the population mean is 505, the sample size is 64, and the population standard deviation is known to be 36

A one-tailed hypothesis for a population mean with a significance level equal to .05 will have a critical value equal to z = .45.

The chance of making a Type II statistical error increases if the "true" population mean is closer to the hypothesized population mean, all other factors held constant.

A company that sells an online course aimed at helping high-school students improve their SAT scores has claimed that SAT scores will improve by more than 90 points on average if students successfully complete the course. To test this, a national school counseling organization plans to select a random sample of n = 100 students who have previously taken the SAT test. These students will take the company's course and then retake the SAT test. Assuming that the population standard deviation for improvement in test scores is thought to be 30 points and the level of significance for the hypothesis test is 0.05, what is the probability that the counseling organization will incorrectly "accept" the null hypothesis when, in fact, the true mean increase is actually 95 points?

Suppose a recent random sample of employees nationwide that have a 401(k) retirement plan found that 18% of them had borrowed against it in the last year. A random sample of 100 employees from a local company who have a 401(k) retirement plan found that 14 had borrowed from their plan. Based on the sample results, is it possible to conclude, at the α = 0.025 level of significance, that the local company had a lower proportion of borrowers from its 401(k) retirement plan than the 18% reported nationwide?

For the following hypothesis test:

A two-tailed hypothesis test with α = 0.05 is similar to a 95 percent confidence interval.

Choosing an alpha of 0.01 will cause beta to equal 0.99.

Explain why an increase in sample size will reduce the probability of a Type II error but will not impact the probability of a Type I error.

According to data from the Environmental Protection Agency, the average daily water consumption for a household of four people in the United States is approximately at least 243 gallons. (Source: http://www.catskillcenter.org/programs/csp/H20/Lesson3/house3.htm) Suppose a state agency plans to test this claim using an alpha level equal to 0.05 and a random sample of 100 households with four people. Calculate the probability of committing a Type II error if the true population mean is 230 gallons. Assume that the population standard deviation is known to be 40 gallons.

Woof Chow Dog Food Company believes that it has a market share of 25 percent. It surveys n = 100 dog owners and ask whether or not Woof Chow is their regular brand of dog food, and 23 people say yes. Based upon this information, what is the critical value if the hypothesis is to be tested at the 0.05 level of significance?

According to CNN business partner Careerbuilder.com, the average starting salary for accounting graduates in 2008 was at least $47,413. Suppose that the American Society for Certified Public Accountants planned to test this claim by randomly sampling 200 accountants who graduated in 2008. Compute the power of the hypothesis test to reject the null hypothesis if the true average starting salary is only $47,000. Assume that the population standard deviation is known to be $4,600 and the test is to be conducted using an alpha level equal to 0.01.