Exam 9: Introduction to Hypothesis Testing

Nationwide Mutual Insurance, based in Columbus, Ohio, is one of the largest diversified insurance and financial services organizations in the world, with more than $157 billion in assets. Nationwide ranked 108th on the Fortune 100 list in 2008. The company provides a full range of insurance and financial services. In a recent news release Nationwide reported the results of a new survey of 1,097 identity theft victims. The survey shows victims spend an average of 81 hours trying to resolve their cases. If the true average time spent was 81 hours, determine the probability that a test of hypothesis designed to test that the average was less than 85 hours would reject the research hypothesis. Use α= 0.05 and a standard deviation of 50.

The director of a state agency believes that the average starting salary for clerical employees in the state is less than $30,000 per year. To test her hypothesis, she has collected a simple random sample of 100 starting clerical salaries from across the state and found that the sample mean is $29,750. Assuming the population standard deviation is known to be $2,500 and the significance level for the test is to be 0.05, what is the critical value (stated in dollars)?

In a two-tailed hypothesis test for a population mean, an increase in the sample size will:

The makers of Mini-Oats Cereal have an automated packaging machine that can be set at any targeted fill level between 12 and 32 ounces. Every box of cereal is not expected to contain exactly the targeted weight, but the average of all boxes filled should. At the end of every shift (eight hours), 16 boxes are selected at random and the mean and standard deviation of the sample are computed. Based on these sample results, the production control manager determines whether the filling machine needs to be readjusted or whether it remains all right to operate. Use α = 0.05. Establish the appropriate null and alternative hypotheses to be tested for boxes that are supposed to have an average of 24 ounces.

After completing sales training for a large company, it is expected that the salesperson will generate a sale on at least 15 percent of the calls he or she makes. To make sure that the sales training process is working, a random sample of n = 400 sales calls made by sales representatives who have completed the training have been selected and the null hypothesis is to be tested at 0.05 alpha level. Suppose that a sale is made on 36 of the calls. Based on these sample data, which of the following is true?

Because of the complex nature of the U.S. income tax system, many people have questions for the Internal Revenue Service (IRS). Yet, an article published by the Detroit Free Press entitled "Assistance: IRS Help Centers Give the Wrong Information" discusses the propensity of IRS staff employees to give incorrect tax information to tax-payers who call with questions. Then IRS Inspector General Pamela Gardiner told a Senate subcommittee that "the IRS employees at 400 taxpayer assistance centers nationwide encountered 8.5 million taxpayers face-to-face last year. The problem: When inspector general auditors posing as taxpayers asked them to answer tax questions, the answers were right 69% of the time." Suppose an independent commission was formed to test whether the 0.69 accuracy rate is correct or whether it is actually higher or lower. The commission has randomly selected n = 180 tax returns that were completed by IRS assistance employees and found that 105 of the returns were accurately completed. State the appropriate null and alternative hypotheses.

Lube-Tech is a major chain whose primary business is performing lube and oil changes for passenger vehicles. The national operations manager has stated in an industry newsletter that the mean number of miles between oil changes for all passenger cars exceeds 4,200 miles. To test this, an industry group has selected a random sample of 100 vehicles that have come into a lube shop and determined the number of miles since the last oil change and lube. The sample mean was 4,278 and the standard deviation was known to be 780 miles. Based on a significance level of 0.10, the critical value for the test is approximately z = 1.28.

Given the following null and alternative 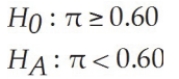Test the hypothesis using α = 0.01 assuming that a sample of n = 200 yielded x = 105 items with the desired attribute.

You are given the following null and alternative hypotheses: 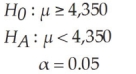If the true population mean is 4,345, determine the value of beta. Assume the population standard deviation is known to be 200 and the sample size is 100.

Aceco has a contract with a supplier to ship parts that contain no more than three percent defects. When a large shipment of parts comes in, Aceco samples n = 150. Based on the results of the sample, they either accept the shipment or reject it. If Aceco wants no more than a 0.10 chance of rejecting a good shipment, the cut-off between accepting and rejecting should be 0.0478 or 4.78 percent of the sample.

If the p value is less than α in a two-tailed test,

A sample is used to obtain a 95 percent confidence interval for the mean of a population. The confidence interval goes from 15 to 19. If the same sample had been used to test the null hypothesis that the mean of the population is equal to 20 versus the alternative hypothesis that the mean of the population differs from 20, the null hypothesis could be rejected at a level of significance of 0.05.

A mail-order business prides itself in its ability to fill customers' orders in six calendar days or less on the average. Periodically, the operations manager selects a random sample of customer orders and determines the number of days required to fill the orders. Based on this sample information, he decides if the desired standard is not being met. He will assume that the average number of days to fill customers' orders is six or less unless the data suggest strongly otherwise. On one occasion where a sample of 40 customers was selected, the average number of days was 6.65, with a sample standard deviation of 1.5 days. Can the operations manager conclude that his mail-order business is achieving its goal? Use a significance level of 0.025 to answer this question.

A recent report in which a major pharmaceutical company released the results of testing that had been done on the cholesterol reduction that people could expect if they use the company's new drug indicated that the Type II error probability for a given "true" mean was 0.1250 based on the sample size of n = 64 subjects. Given this, what was the power of the test under these same conditions? The alpha level used in the test was 0.05.

A company that makes shampoo wants to test whether the average amount of shampoo per bottle is 16 ounces. The standard deviation is known to be 0.20 ounces. Assuming that the hypothesis test is to be performed using 0.10 level of significance and a random sample of n = 64 bottles, which of the following would be the upper tail critical value?

For the following hypothesis test:

A major package delivery company claims that at least 95 percent of the packages it delivers reach the destination on time. As part of the evidence in a lawsuit against the package company, a random sample of n = 200 packages was selected. A total of 188 of these packages were delivered on time. Using a significance level of 0.05, the critical value for this hypothesis test is approximately 0.90.

The Center on Budget and Policy Priorities (www.cbpp.org) reported that average out-of-pocket medical expenses for prescription drugs for privately insured adults with incomes over 200% of the poverty level was $173 in 2002. Suppose an investigation was conducted in 2012 to determine whether the increased availability of generic drugs, Internet prescription drug purchases, and cost controls have reduced out-of-pocket drug expenses. The investigation randomly sampled 196 privately insured adults with incomes over 200% of the poverty level, and the respondents' 2012 out-of-pocket medical expenses for prescription drugs were recorded. These data are in the file Drug Expenses. Based on the sample data, can it be concluded that 2012 out-of-pocket prescription drug expenses are lower than the 2002 average reported by the Center on Budget and Policy Priorities? Use a level of significance of 0.01 to conduct the hypothesis test.

A consumer group plans to test whether a new passenger car that is advertised to have a mean highway miles per gallon of at least 33 actually meets this level. They plan to test the hypothesis using a significance level of 0.05 and a sample size of n = 100 cars. It is believed that the population standard deviation is 3 mpg. Based upon this information, if the "true" population mean is 32.0 mpg, what is the probability that the test will lead the consumer group to "accept" the claimed mileage for this car?

The director of the city Park and Recreation Department claims that the mean distance people travel to the city's greenbelt is more than 5.0 miles. Assuming that the population standard deviation is known to be 1.2 miles and the significance level to be used to test the hypothesis is 0.05 when a sample size of n = 64 people are surveyed, the probability of a Type II error is approximately .4545 when the "true" population mean is 5.5 miles.