Exam 9: Introduction to Hypothesis Testing

An article in an operations management journal recently stated that a formal hypothesis test rejected the hypothesis that mean employee productivity was less than $45.70 per hour in the wood processing industry. Given this conclusion, it is possible that a Type I statistical error was committed.

The cost of a college education has increased at a much faster rate than costs in general over the past twenty years. In order to compensate for this, many students work part- or full-time in addition to attending classes. At one university, it is believed that the average hours students work per week exceeds 20. To test this at a significance level of 0.05, a random sample of n = 20 students was selected and the following values were observed: 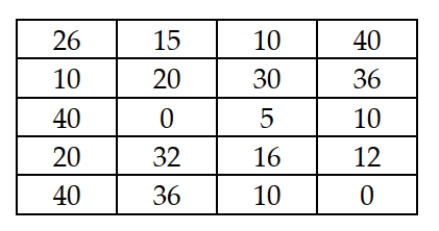Based on these sample data, which of the following statements is true?

A company that sells an online course aimed at helping high-school students improve their SAT scores has claimed that SAT scores will improve by more than 90 points on average if students successfully complete the course. To test this, a national school counseling organization plans to select a random sample of n = 100 students who have previously taken the SAT test. These students will take the company's course and then retake the SAT test. Assuming that the population standard deviation for improvement in test scores is thought to be 30 points and the level of significance for the hypothesis test is 0.05, find the critical value in terms of improvement in SAT points, which would be needed prior to finding a beta.

A company that makes and markets a device that is aimed at helping people quit smoking claims that at least 70 percent of the people who have used the product have quit smoking. To test this, a random sample of n = 100 product users was selected. The critical value for the hypothesis test using a significance level of 0.05 would be approximately -1.645.

The executive director of the United Way believes that more than 24 percent of the employees in the high-tech industry have made voluntary contributions to the United Way. In order to test this statistically, the appropriate null and alternative hypotheses are: H0 : ≤ .24 HA : > .24

Lube-Tech is a major chain whose primary business is performing lube and oil changes for passenger vehicles. The national operations manager has stated in an industry newsletter that the mean number of miles between oil changes for all passenger cars exceeds 4,200 miles. To test this, an industry group has selected a random sample of 100 vehicles that have come into a lube shop and determined the number of miles since the last oil change and lube. The sample mean was 4,278 and the standard deviation was known to be 780 miles. Based on this information, the p-value for the hypothesis test is less than 0.10.

A company makes a device that can be fitted to automobile engines to improve the mileage. The company claims that if the device is installed, owners will observe a mean increase of more than 3.0 mpg. Assuming that the population standard deviation of increase is known to be 0.75 mpg, and a sample of size 64 cars is selected, what is the probability of "accepting" the null hypothesis if the true population mean is 3.10 mpg increase? Assume that the test will be performed using a 0.05 level of significance.

In a hypothesis test, the p-value measures the probability that the alternative hypothesis is true.

The produce manager for a large retail grocery store believes that an average head of lettuce weighs more than 1.7 pounds. If she were to test this statistically, what would the null and alternative hypotheses be and what is the research hypothesis?

The power of a test is measured by its capability of:

The following is an appropriate statement of the null and alternate hypotheses for a test of a population mean: H0 : μ = 45 HA : μ < 50

The significance level in a hypothesis test corresponds to the maximum probability that a Type I error will be committed.

According to CNN business partner Careerbuilder.com, the average starting salary for accounting graduates in 2008 was at least $47,413. Suppose that the American Society for Certified Public Accountants planned to test this claim by randomly sampling 200 accountants who graduated in 2008. State the appropriate null and alternative hypotheses.

A cell phone company believes that 90 percent of their customers are satisfied. They survey a sample of n = 100 customers and find that 82 say they are satisfied. In calculating the standard error of the sampling distribution (σp) the proportion to use is 0.82.

For the following hypothesis test 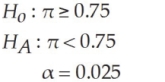With n = 100 and p = 0.66, state the decision rule in terms of the critical value of the test statistic

If we are performing a two-tailed test of whether μ = 100, the probability of detecting a shift of the mean to 105 will be ________ the probability of detecting a shift of the mean to 110.

One of the factors that a company will use in determining whether it will locate a new facility in a community is the status of the real estate market. The managers believe that an important measure of the real estate market is the average length of time that homes stay on the market before selling. They believe that if the mean time on the market is less than 45 days, the real estate market is favorable. To test this in a particular area, a random sample of n = 100 homes that sold during the past six months was selected. The mean for this sample was 40 days. It is believed that the population standard deviation is 15 days. If the test is conducted using a 0.05 level of significance, what conclusion should be reached?

The Gordon Beverage Company bottles soft drinks using an automatic filling machine. When the process is running properly, the mean fill is 12 ounces per can. The machine has a known standard deviation of 0.20 ounces. Each day, the company selects a random sample of 36 cans and measures the volume in each can. They then test to determine whether the filling process is working properly. The test is conducted using a 0.05 significance level. What is the critical value in ounces?

The Gordon Beverage Company bottles soft drinks using an automatic filling machine. When the process is running properly, the mean fill is 12 ounces per can. The machine has a known standard deviation of 0.20 ounces. Each day, the company selects a random sample of 36 cans and measures the volume in each can. They then test to determine whether the filling process is working properly. The test is conducted using a 0.05 significance level. Using the test statistic approach, what conclusion should the company reach if the sample mean is 12.02 ounces? What type of statistical error may have been committed?

For the following hypothesis test: