Exam 6: Work and Kinetic Energy
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Energy conservation with nonconservative forces: A 50.0-kg skier starting from rest travels 200 m down a hill that has a 20.0° slope and a uniform surface. When the skier reaches the bottom of the hill, her speed is 30.0 m/s.
(a) How much work is done by friction as the skier comes down the hill?
(b) What is the magnitude of the friction force if the skier travels directly down the hill?
Free
(Essay)
4.7/5  (38)
(38)
Correct Answer:
(a) -1.10 × 104 J
(b) 55.3 N
Work-energy theorem: In the figure, two boxes, each of mass 24 kg, are at rest and connected as shown. The coefficient of kinetic friction between the inclined surface and the box is 0.31. Find the speed of the boxes just after they have moved 1.6 m. 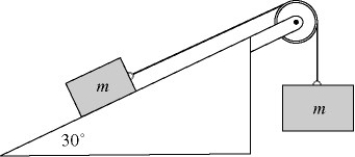
Free
(Short Answer)
4.8/5  (28)
(28)
Correct Answer:
1.9 m/s
Energy conservation with conservative forces: Swimmers at a water park have a choice of two frictionless water slides as shown in the figure. Although both slides drop over the same height, h, slide 1 is straight while slide 2 is curved, dropping quickly at first and then leveling out. How does the speed v1 of a swimmer reaching the end of slide 1 compares with v2, the speed of a swimmer reaching the end of slide 2? 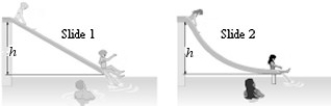
Free
(Multiple Choice)
4.9/5  (43)
(43)
Correct Answer:
C
Energy conservation with nonconservative forces: A girl throws a stone from a bridge. Consider the following ways she might throw the stone. The speed of the stone as it leaves her hand is the same in each case, and air resistance is negligible. Case A: Thrown straight up.
Case B: Thrown straight down.
Case C: Thrown out at an angle of 45° above horizontal.
Case D: Thrown straight out horizontally.
In which case will the speed of the stone be greatest when it hits the water below?
(Multiple Choice)
4.9/5  (33)
(33)
Work-energy theorem: A 5.00-kg box slides 4.00 m across the floor before coming to rest. What is the coefficient of kinetic friction between the floor and the box if the box had an initial speed of 3.00 m/s?
(Multiple Choice)
4.8/5  (36)
(36)
Energy conservation with conservative forces: A box of mass m is pressed against (but is not attached to) an ideal spring of force constant k and negligible mass, compressing the spring a distance x. After it is released, the box slides up a frictionless incline as shown in the figure and eventually stops. If we repeat this experiment but instead compress the spring a distance of 2x 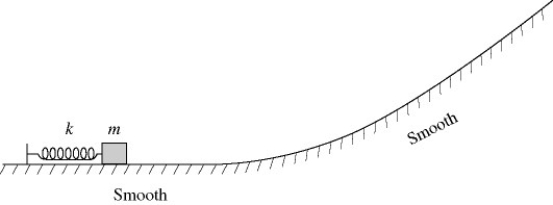
(Multiple Choice)
4.9/5  (31)
(31)
Energy conservation with conservative forces: It requires 6.0 J of work is needed to push a 2.0-kg object from point A to point B of the frictionless ramp as shown in the figure. What is the length s of the ramp from A to B? 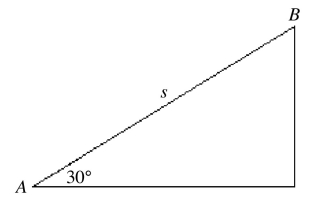
(Short Answer)
4.9/5  (34)
(34)
Work done by variable forces: A force on a particle depends on position such that F(x) = (3.00 N/ 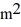 )
) 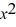 + ( 6.00 N/m)x for a particle constrained to move along the x-axis. What work is done by this force on a particle that moves from x = 0.00 m to x = 2.00 m?
+ ( 6.00 N/m)x for a particle constrained to move along the x-axis. What work is done by this force on a particle that moves from x = 0.00 m to x = 2.00 m?
(Multiple Choice)
4.7/5  (44)
(44)
Energy conservation with conservative forces: A very small 100-g object is attached to one end of a massless 10-cm rod that is pivoted without friction about the opposite end. The rod is held vertical, with the object at the top, and released, allowing the rod to swing. What is the speed of the object at the instant that the rod is horizontal?
(Multiple Choice)
4.8/5  (36)
(36)
Power: The work performed as a function of time for a process is given by 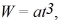 where
where 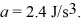 What is the instantaneous power output at
What is the instantaneous power output at 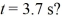
(Multiple Choice)
4.9/5  (41)
(41)
Energy conservation with conservative forces: An 8.0-m massless rod is loosely pinned to a frictionless pivot at 0, as shown in the figure. A very small 4.0-kg ball is attached to the other end of the rod. The ball is held at A, where the rod makes a 30° angle above the horizontal, and is released. The ball-rod assembly then swings freely with negligible friction in a vertical circle between A and B. The tension in the rod when the ball passes through the lowest point at D is closest to 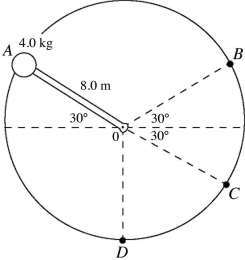
(Multiple Choice)
4.7/5  (36)
(36)
Energy conservation with nonconservative forces: A 5.00-kg object moves clockwise around a 50.0 cm radius circular path. At one location, the speed of the object is 4.00 m/s. When the object next returns to this same location, the speed is 3.00 m/s.
(a) How much work was done by nonconservative (dissipative) forces as the object moved once around the circle?
(b) If the magnitude of the above nonconservative (dissipative) forces acting on the object is constant, what is the value of this magnitude?
(Essay)
4.9/5  (32)
(32)
Force and potential energy: The plot in the figure shows the potential energy of a particle, due to the force exerted on it by another particle, as a function of distance. At which of the three points labeled in the figure is the magnitude of the force on the particle greatest? 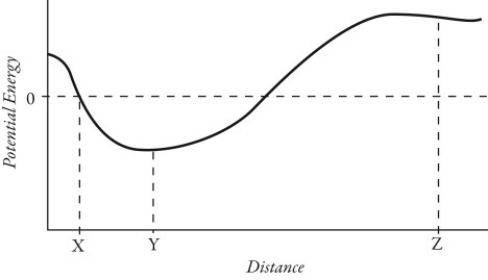
(Multiple Choice)
4.7/5  (37)
(37)
Work done by variable forces: In the figure, two identical springs have unstretched lengths of 0.25 m and spring constants of 300 N/m. The springs are attached to a small cube and stretched to a length L of 0.36 m as in Figure A. An external force P pulls the cube a distance D = 0.020 m to the right and holds it there. (See Figure B.) The work done by the external force P in pulling the cube 0.020 m is closest to 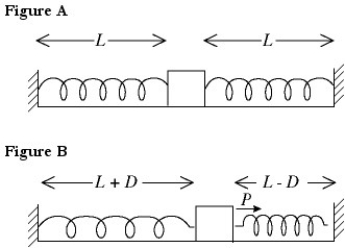
(Multiple Choice)
4.9/5  (37)
(37)
Energy conservation with conservative forces: A box of mass m is pressed against (but is not attached to) an ideal spring of force constant k and negligible mass, compressing the spring a distance x. After it is released, the box slides up a frictionless incline as shown in the figure and eventually stops. If we repeat this experiment but instead use a spring having force constant 2k 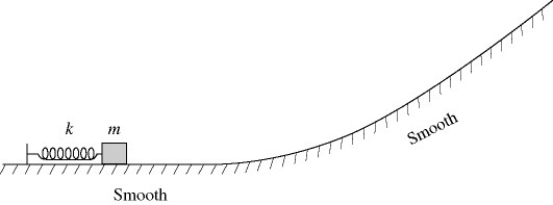
(Multiple Choice)
4.9/5  (41)
(41)
Gravitational potential energy: You do 174 J of work while pulling your sister back on a swing, whose chain is 5.10 m long. You start with the swing hanging vertically and pull it until the chain makes an angle of 32.0° with the vertical with your sister is at rest. What is your sister's mass, assuming negligible friction?
(Multiple Choice)
4.9/5  (35)
(35)
Work: A traveler pulls on a suitcase strap at an angle 36° above the horizontal. If  of work are done by the strap while moving the suitcase a horizontal distance of 15 m, what is the tension in the strap?
of work are done by the strap while moving the suitcase a horizontal distance of 15 m, what is the tension in the strap?
(Multiple Choice)
4.7/5  (29)
(29)
Hooke's law: Block A (0.40 kg) and block B (0.30 kg) are on a frictionless table (see figure). Spring 1 connects block A to a frictionless peg at 0 and spring 2 connects block A and block B. When the blocks are in uniform circular motion about 0, the springs have lengths of 0.60 m and 0.40 m, as shown. The springs are ideal and massless, and the linear speed of block B is 2.0 m/s. If the distance that spring 2 stretches is 0.060 m, the spring constant of spring 2 is closest to 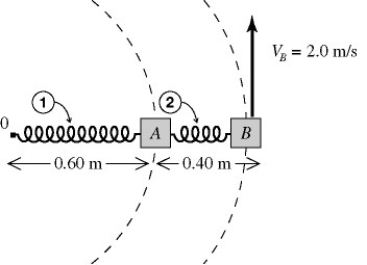
(Multiple Choice)
5.0/5  (34)
(34)
Work: A force 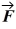 = 12 N
= 12 N  - 10 N
- 10 N  acts on an object. How much work does this force do as the object moves from the origin to the point
acts on an object. How much work does this force do as the object moves from the origin to the point 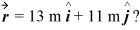
(Multiple Choice)
4.7/5  (26)
(26)
Work: A stock person at the local grocery store has a job consisting of the following five segments: (1) picking up boxes of tomatoes from the stockroom floor
(2) accelerating to a comfortable speed
(3) carrying the boxes to the tomato display at constant speed
(4) decelerating to a stop
(5) lowering the boxes slowly to the floor.
During which of the five segments of the job does the stock person do positive work on the boxes?
(Multiple Choice)
4.9/5  (37)
(37)
Showing 1 - 20 of 109
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)