Exam 33: The Nature and Propagation of Light

Molecular rotation: A diatomic molecule has a moment of inertia of 7.73 × 10^-45 kg∙ m². What is its rotational energy in the quantum state characterized by l = 2? (h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J)

Free-electron theory of metals: Silver has a Fermi level (energy) of 5.5 eV. At 0 K, at what speed would the electrons be moving if they had kinetic energy equal to the Fermi energy? (This speed is known as the Fermi speed.) (m_el = 9.11 × 10^-31 kg, 1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s)

Molecular rotation: The spacing of the atoms (treated as point masses) in the H₂ molecule is 7.4 × 10^-11 m. What is the energy of the l = 1 rotational level? (1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, m_h ≈ m_proton = 1.67 × 10^-27 kg)

Molecular rotation: When a certain diatomic molecule undergoes a transition from the l = 5 to the l = 3 rotational level, the emitted photon has wavelength 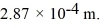Calculate the moment of inertia of the molecule. (c = 3.00 × 10⁸ m/s, e = 1.60 × 10^-19 C, h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s)

Semiconductors: A p-type semiconductor has a net positive charge.

Free-electron theory of metals: What is the occupancy probability at an energy of 12.00 eV for a material with a Fermi energy (level) of 11.63 eV at a temperature of 500 K? (m_el = 9.11 × 10^-31 kg, h = 6.626 × 10^-34 J ∙ s, Boltzmann constant = 1.38 × 10^-23, 1 eV = 1.60 × 10^-19 J)

Free-electron theory of metals: If one metal has double the number of conduction electrons per unit volume of a second metal, then its Fermi level (energy) is how many times that of the second metal?

Molecular rotation: A diatomic molecule has 18 × 10^-5 eV of rotational energy in the l = 2 quantum state. What is its rotational energy in the l = 0 quantum state?

Free-electron theory of metals: A metal has a Fermi level (energy) of 5.50 eV. At 1200 K, what energy will have a 90% occupancy probability? (m_el = 9.11 × 10^-31 kg, h = 6.626 × 10^-34 J ∙ s, Boltzmann constant = 1.38 × 10^-23, 1 eV = 1.60 × 10^-19 J)

Molecular vibration: The vibrational frequency of an HF molecule is 8.72 × 10¹³ Hz and the reduced mass of the molecule is 1.589 × 10^-27 kg. What is the ground state vibrational energy of an HF molecule? (1 eV = 1.60 × 10^-19 J, ħ = 1.055 × 10^-34 J ∙ s, h = 6.626 × 10^-34 J ∙ s)

Molecular vibration: A certain diatomic molecule emits a photon of energy 1.20 eV when it makes a transition from the n = 1 vibrational state to the next lower vibrational state. What is the frequency of vibration of the molecule? (h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J)

Molecular vibration: A diatomic molecule is vibrating in its first excited quantum state above the ground state. In that excited state, its frequency is 2.0 × 10¹³ Hz. What is the energy of the molecule in this state? (h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J

Molecular vibration: A certain diatomic molecule emits a photon of energy 1.20 eV when it makes a transition from the n = 1 vibrational state to the next lower vibrational state. If the molecule made a transition from the n = 2 state to the n = 1 state, what would be the energy of the photon it would emit? (h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J)

Molecular rotation: A rotating diatomic molecule has rotational quantum number l. The energy DIFFERENCE between adjacent energy levels

Free-electron theory of metals: The Fermi level (energy) of a metal is 5.5 eV. What is the number of conduction electrons per unit volume for this metal? (m_el = 9.11 × 10^-31 kg, 1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s)

Free-electron theory of metals: The Fermi energy of rubidium at a temperature of 5 K is 1.85 eV. An electron state in rubidium is 0.007 eV above the Fermi level. What is the probability that this state is occupied at a temperature of 9K? (m_el = 9.11 × 10^-31 kg, h = 6.626 × 10^-34 J ∙ s, Boltzmann constant = 1.38 ∙ 10^-23 J/K, 1 eV = 1.60 × 10^-19 J)

Molecular rotation: The moment of inertia of a fluorine ( 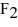) molecule is 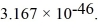What is the rotational energy of a fluorine molecule for the l = 19 state? (h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, 1 eV = 1.60 × 10^-19 J)

Semiconductors: An unfilled electron state in the valence band is called

Molecular rotation: Estimate the rotational energy (in eV) for a diatomic hydrogen molecule in the l = 2 quantum state. (The equilibrium separation for the H₂ molecule is 0.074 nm.) (1 eV = 1.60 × 10^-19 J, h = 6.626 × 10^-34 J ∙ s, ħ = 1.055 × 10^-34 J ∙ s, m_h ≈ m_proton = 1.67 × 10^-27 kg)

Molecular bonds: Ionic bonding is due to