Exam 4: Newtons Laws of Motion
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Projectiles: A boy throws a rock with an initial velocity of 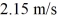 at 30.0° above the horizontal. If air resistance is negligible, how long does it take for the rock to reach the maximum height of its trajectory?
at 30.0° above the horizontal. If air resistance is negligible, how long does it take for the rock to reach the maximum height of its trajectory?
Free
(Multiple Choice)
4.9/5  (28)
(28)
Correct Answer:
A
Projectiles: A projectile is fired from point 0 at the edge of a cliff, with initial velocity components of v0x = 60.0 m/s and v0y = 175 m/s, as shown in the figure. The projectile rises and then falls into the sea at point P. The time of flight of the projectile is 40.0 s, and it experiences no appreciable air resistance in flight. What is the height of the cliff? 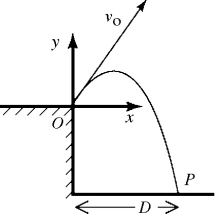
Free
(Short Answer)
4.7/5  (36)
(36)
Correct Answer:
840 m
Relative velocity: A swimmer heading directly across a river 200 m wide reaches the opposite bank in 6 min 40 s, during which time she is swept downstream 480 m.
(a) How fast can she swim in still water?
(b) What is the speed of the current?
Free
(Essay)
4.8/5  (24)
(24)
Correct Answer:
(a) 0.50 m/s
(b) 1.2 m/s
Two-dimensional motion: If you set the cruise control of your car to a certain speed and take a turn, the speed of the car will remain the same. Is the car accelerating?
(Multiple Choice)
4.9/5  (29)
(29)
Projectiles: A rescue plane flying horizontally at 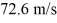 spots a survivor in the ocean
spots a survivor in the ocean 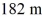 directly below and releases an emergency kit with a parachute. . Because of the shape of the parachute, it experiences insignificant horizontal air resistance. If the kit descends with a constant vertical acceleration of
directly below and releases an emergency kit with a parachute. . Because of the shape of the parachute, it experiences insignificant horizontal air resistance. If the kit descends with a constant vertical acceleration of 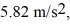 how far away from the survivor will it hit the waves?
how far away from the survivor will it hit the waves?
(Multiple Choice)
4.9/5  (37)
(37)
Projectiles: For general projectile motion, when the projectile is at the highest point of its trajectory
(Multiple Choice)
4.7/5  (28)
(28)
Two-dimensional motion: An electron moves with a constant horizontal velocity of 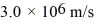 and no initial vertical velocity as it enters a deflector inside a TV tube. The electron strikes the screen after traveling
and no initial vertical velocity as it enters a deflector inside a TV tube. The electron strikes the screen after traveling 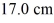 horizontally and
horizontally and 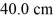 vertically upward with no horizontal acceleration. What is the constant vertical acceleration provided by the deflector? (The effects of gravity can be ignored.)
vertically upward with no horizontal acceleration. What is the constant vertical acceleration provided by the deflector? (The effects of gravity can be ignored.)
(Multiple Choice)
4.9/5  (42)
(42)
Two-dimensional motion: Shown below are the velocity and acceleration vectors for a person in several different types of motion. In which case is the person slowing down and turning to his right?
(Multiple Choice)
4.8/5  (33)
(33)
Uniform circular motion: A wind farm generator uses a two-bladed propeller (see figure) mounted on a pylon at a height of 20 m. The length of each propeller blade is 12 m. A small piece from the tip of the propeller breaks off when the propeller is vertical. At that instant, the period of the motion of the propeller is 1.2 s. The fragment flies off horizontally, falls with negligible air resistance, and strikes the ground at P.
(a) How far is point P from the base of the pylon?
(b) At what angle with respect to the vertical is the fragment moving just as it strikes the ground at P? 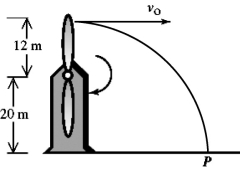
(Essay)
4.8/5  (31)
(31)
Uniform circular motion: An object moves in a circle of radius R at constant speed with a period T. If you want to change only the period in order to cut the object's acceleration in half, the new period should be
(Multiple Choice)
4.7/5  (31)
(31)
Uniform circular motion: A satellite orbits the earth a distance of 1.50 × 107 m above the planet's surface and takes 8.65 hours for each revolution about the earth. The earth's radius is 6.38 × 106 m. The acceleration of this satellite is closest to
(Multiple Choice)
4.7/5  (31)
(31)
Two-dimensional motion: Object A has a position as a function of time given by 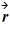 A(t) = (3.00 m/s)t
A(t) = (3.00 m/s)t  + (1.00 m/s2)t2
+ (1.00 m/s2)t2
 . Object B has a position as a function of time given by
. Object B has a position as a function of time given by 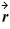 B(t) = (4.00 m/s)t
B(t) = (4.00 m/s)t  + (-1.00 m/s2)t2
+ (-1.00 m/s2)t2
 . All quantities are SI units. What is the distance between object A and object B at time
. All quantities are SI units. What is the distance between object A and object B at time 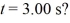
(Multiple Choice)
4.9/5  (33)
(33)
Projectiles: Jan and Len throw identical rocks off a tall building at the same time. The ground near the building is flat. Jan throws her rock straight downward. Len throws his rock downward and outward such that the angle between the initial velocity of the rock and the horizon is 30°. Len throws the rock with a speed twice that of Jan's rock. If air resistance is negligible, which rock hits the ground first?
(Multiple Choice)
4.9/5  (34)
(34)
Relative velocity: A long-distance swimmer is able to swim through still water at 4.0 km/h. She wishes to try to swim from Port Angeles, Washington, directly north to Victoria, British Columbia, a distance of 50 km. An ocean current flows through the Strait of Juan de Fuca from west to east at 3.0 km/h. In what direction (relative to north) should she swim to make the crossing along a straight line between the two cities?
(Multiple Choice)
4.8/5  (34)
(34)
Relative velocity: You want to swim straight across a river that is 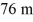 wide. You find that you can do this if you swim at an angle of θ = 28° from the upstream direction at a constant rate of
wide. You find that you can do this if you swim at an angle of θ = 28° from the upstream direction at a constant rate of 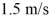 relative to the water. At what rate does the river flow? The angle θ is measured from the river bank (directly upstream is
relative to the water. At what rate does the river flow? The angle θ is measured from the river bank (directly upstream is 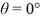 while directly across the river is
while directly across the river is 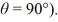
(Multiple Choice)
4.9/5  (32)
(32)
Two-dimensional motion: An object has a position given by ![Two-dimensional motion: An object has a position given by = [2.0 m + ( 5.00 m/s)t] + [3.0 m - ( 2.00 m/s<sup>2</sup>)t<sup>2</sup>] , where quantities are in SI units. What is the speed of the object at time](https://storage.examlex.com/TB8274/11eb6b7b_2f2c_8c82_b0cf_c1fa86cf08cc_TB8274_11.jpg) = [2.0 m + ( 5.00 m/s)t]
= [2.0 m + ( 5.00 m/s)t] ![Two-dimensional motion: An object has a position given by = [2.0 m + ( 5.00 m/s)t] + [3.0 m - ( 2.00 m/s<sup>2</sup>)t<sup>2</sup>] , where quantities are in SI units. What is the speed of the object at time](https://storage.examlex.com/TB8274/11eb6b7b_2f2c_8c83_b0cf_2b985a3c84a1_TB8274_11.jpg) + [3.0 m - ( 2.00 m/s2)t2]
+ [3.0 m - ( 2.00 m/s2)t2] ![Two-dimensional motion: An object has a position given by = [2.0 m + ( 5.00 m/s)t] + [3.0 m - ( 2.00 m/s<sup>2</sup>)t<sup>2</sup>] , where quantities are in SI units. What is the speed of the object at time](https://storage.examlex.com/TB8274/11eb6b7b_2f2c_8c84_b0cf_ffbd8e6ab6b2_TB8274_11.jpg) , where quantities are in SI units. What is the speed of the object at time
, where quantities are in SI units. What is the speed of the object at time ![Two-dimensional motion: An object has a position given by = [2.0 m + ( 5.00 m/s)t] + [3.0 m - ( 2.00 m/s<sup>2</sup>)t<sup>2</sup>] , where quantities are in SI units. What is the speed of the object at time](https://storage.examlex.com/TB8274/11eb6b7b_2f2c_8c85_b0cf_1537237d81bd_TB8274_11.jpg)
(Multiple Choice)
4.9/5  (30)
(30)
Projectiles: Alice and Tom dive from an overhang into the lake below. Tom simply drops straight down from the edge, but Alice takes a running start and jumps with an initial horizontal velocity of 25 m/s. Neither person experiences any significant air resistance. Just as they reach the lake below
(Multiple Choice)
4.6/5  (26)
(26)
Projectiles: A plane flying at 70.0 m/s suddenly stalls. If the acceleration during the stall is 9.8 m/s2 directly downward, the stall lasts 5.0 s, and the plane was originally climbing at 25° to the horizontal, what is the velocity after the stall?
(Multiple Choice)
4.9/5  (39)
(39)
Projectiles: A child throws a ball with an initial speed of 8.00 m/s at an angle of 40.0° above the horizontal. The ball leaves her hand 1.00 m above the ground and experience negligible air resistance.
(a) What is the magnitude of the ball's velocity just before it hits the ground?
(b) At what angle below the horizontal does the ball approach the ground?
(Essay)
4.9/5  (32)
(32)
Uniform circular motion: For an object in uniform circular motion, its velocity and acceleration vectors are always perpendicular to each other at every point in the path.
(True/False)
4.8/5  (32)
(32)
Showing 1 - 20 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)