Exam 18: Thermal Properties of Matter
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Spheres of charge: The graph in the figure shows the electric field strength (not the field lines) as a function of distance from the center for a pair of concentric uniformly charged spheres. Which of the following situations could the graph plausibly represent? (There may be more than one correct choice.) 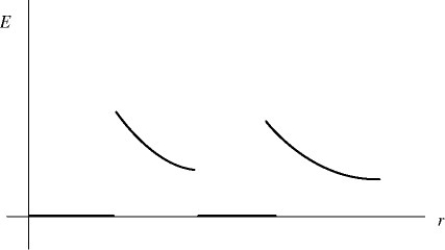
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
A
Charge on conductors: An uncharged conductor has a hollow cavity inside of it. Within this cavity there is a charge of +10 µC that does not touch the conductor. There are no other charges in the vicinity. Which statement about this conductor is true? (There may be more than one correct choice.)
Free
(Multiple Choice)
4.8/5  (22)
(22)
Correct Answer:
D
Charge on conductors: A hollow conducting spherical shell has radii of 0.80 m and 1.20 m, as shown in the figure. The sphere carries an excess charge of -500 nC. A point charge of +300 nC is present at the center. The surface charge density on the inner spherical surface is closest to 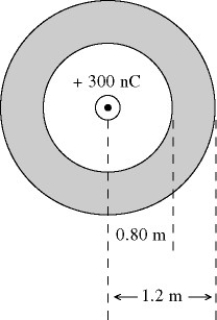
Free
(Multiple Choice)
4.9/5  (41)
(41)
Correct Answer:
D
Sheets of charge: A huge (essentially infinite) horizontal nonconducting sheet 10.0 cm thick has charge uniformly spread over both faces. The upper face carries +95.0 nC/m2 while the lower face carries -25.0 nC/m2. What is the magnitude of the electric field at a point within the sheet 2.00 cm below the upper face? (ε0 = 8.85 × 10-12 C2/N ∙ m2)
(Multiple Choice)
4.7/5  (37)
(37)
Gauss's law: A charge q = 2.00 μC is placed at the origin in a region where there is already a uniform electric field 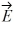 = (100 N/C)
= (100 N/C) 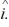 Calculate the flux of the net electric field through a Gaussian sphere of radius R = 10.0 cm centered at the origin. (ε0 = 8.85 × 10-12 C2/N ∙ m2)
Calculate the flux of the net electric field through a Gaussian sphere of radius R = 10.0 cm centered at the origin. (ε0 = 8.85 × 10-12 C2/N ∙ m2)
(Multiple Choice)
4.7/5  (33)
(33)
Sheets of charge: As shown in the figure, a square insulating slab 5.0 mm thick measuring 2.0 m × 2.0 m has a charge of 8.0 × 10-11 C distributed uniformly throughout its volume. Use Gauss's law to determine the electric field at point P, which is located within the slab beneath its center, 1.0 mm from one of the faces. (ε0 = 8.85 × 10-12 C2/N ∙ m2) 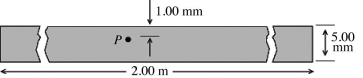
(Multiple Choice)
4.7/5  (36)
(36)
Sheets of charge: Consider two closely spaced and oppositely charged parallel metal plates. The plates are square with sides of length L and carry charges Q and -Q on their facing surfaces. What is the magnitude of the electric field in the region between the plates?
(Multiple Choice)
5.0/5  (28)
(28)
Lines of charge: Two long straight parallel lines, #1 and #2, carry uniform positive linear charge densities. The charge density on line #2 is twice as great as the charge density on line #1. The locus of points where the electric field due to these lines is zero is
(Multiple Choice)
4.7/5  (34)
(34)
Lines of charge: At a distance D from a very long (essentially infinite) uniform line of charge, the electric field strength is 1000 N/C. At what distance from the line will the field strength to be 2000 N/C?
(Multiple Choice)
4.9/5  (37)
(37)
Lines of charge: The cross section of a long coaxial cable is shown in the figure, with radii as given. The linear charge density on the inner conductor is 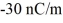 and the linear charge density on the outer conductor is
and the linear charge density on the outer conductor is 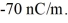 The inner and outer cylindrical surfaces are respectively denoted by A, B, C, and D, as shown.
The inner and outer cylindrical surfaces are respectively denoted by A, B, C, and D, as shown. 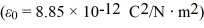 The radial component of the electric field at a point that 34 mm from the axis is closest to
The radial component of the electric field at a point that 34 mm from the axis is closest to 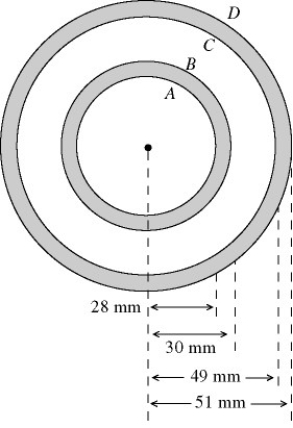
(Multiple Choice)
4.9/5  (38)
(38)
Spheres of charge: A spherical, non-conducting shell of inner radius 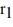 = 10 cm and outer radius
= 10 cm and outer radius 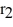 = 15 cm carries a total charge Q = 15 μC distributed uniformly throughout the volume of the shell. What is the magnitude of the electric field at a distance r = 12 cm from the center of the shell? (k = 1/4πε0 = 8.99 × 109 N ∙ m2/C2)
= 15 cm carries a total charge Q = 15 μC distributed uniformly throughout the volume of the shell. What is the magnitude of the electric field at a distance r = 12 cm from the center of the shell? (k = 1/4πε0 = 8.99 × 109 N ∙ m2/C2)
(Multiple Choice)
4.9/5  (34)
(34)
Spheres of charge: Two concentric spheres are shown in the figure. The inner sphere is a solid nonconductor and carries a charge of +5.00 µC uniformly distributed over its outer surface. The outer sphere is a conducting shell that carries a net charge of -8.00 µC. No other charges are present. The radii shown in the figure have the values R1 = 10.0 cm, R2 = 20.0 cm, and R3 = 30.0 cm. (k = 1/4πε0 = 8.99 × 109 N ∙ m2/C2)
(a) Find the total excess charge on the inner and outer surfaces of the conducting sphere.
(b) Find the magnitude and direction of the electric field at the following distances r from the center of the inner sphere: (i) r = 9.5 cm, (ii) r = 15.0 cm, (iii) r = 27.0 cm, (iv) r = 35.0 cm. 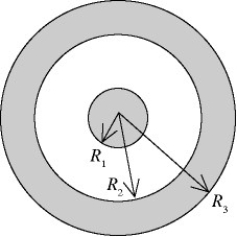
(Essay)
4.8/5  (29)
(29)
Gauss's law: The cube of insulating material shown in the figure has one corner at the origin. Each side of the cube has length 0.080 m so the top face of the cube is parallel to the xz-plane and is at y = 0.080 m. It is observed that there is an electric field 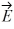 = (3280 N/C ∙ m)y
= (3280 N/C ∙ m)y  that is in the +y direction and whose magnitude depends only on y. Use Gauss's law to calculate the net charge enclosed by the cube. (ε0 = 8.85 × 10-12 C2/N ∙ m2)
that is in the +y direction and whose magnitude depends only on y. Use Gauss's law to calculate the net charge enclosed by the cube. (ε0 = 8.85 × 10-12 C2/N ∙ m2) 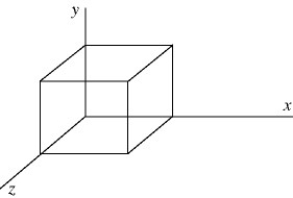
(Short Answer)
4.9/5  (32)
(32)
Charge on conductors: An irregular conductor carries a surface charge density of -6.75 µC/m2 at and in the vicinity of a point P on the surface. An electron is released just above P outside the conductor. What are the magnitude and direction of its acceleration the instant after it is released? (ε0 = 8.85 × 10-12 C2/N ∙ m2, e = 1.60 × 10-19 C, mel = 9.11 × 10-31 kg)
(Essay)
4.9/5  (35)
(35)
Spheres of charge: A nonconducting spherical shell of inner radius R1 and outer radius R2 contains a uniform volume charge density ρ throughout the shell. Use Gauss's law to derive an equation for the magnitude of the electric field at the following radial distances r from the center of the sphere. Your answers should be in terms of ρ, R1, R2, r, ε0 , and π.
(a) r < R1
(b) R1 < r < R2
(c) r > R2
(Essay)
4.7/5  (33)
(33)
Spheres of charge: Electric charge is uniformly distributed inside a nonconducting sphere of radius 0.30 m. The electric field at a point P, which is 0.50 m from the center of the sphere, is 15,000 N/C and is directed radially outward. What is the maximum magnitude of the electric field due to this sphere?
(Multiple Choice)
4.8/5  (35)
(35)
Sheets of charge: Two extremely large nonconducting horizontal sheets each carry uniform charge density on the surfaces facing each other. The upper sheet carries +5.00 µC/m2. The electric field midway between the sheets is 4.25 × 105 N/C pointing downward. What is the surface charge density on the lower sheet? (ε0 = 8.85 × 10-12 C2/N ∙ m2)
(Short Answer)
5.0/5  (39)
(39)
Lines of charge: Charge is distributed uniformly throughout a large insulating cylinder of radius R. The charge per unit length in the cylindrical volume is λ.
(a) Use Gauss's law to find the magnitude of the electric field at a distance r from the central axis of the cylinder for r < R. Your answer should be in terms of r, R, λ, ε0 , and π.
(b) Check the reasonableness of your answer by evaluating it at the surface of the cylinder.
(Essay)
4.9/5  (40)
(40)
Charge on conductors: Under electrostatic conditions, the electric field just outside the surface of any charged conductor
(Multiple Choice)
5.0/5  (31)
(31)
Spheres of charge: A solid nonconducting sphere of radius R carries a charge Q distributed uniformly throughout its volume. At a certain distance r1 (r1 < R) from the center of the sphere, the electric field has magnitude E. If the same charge Q were distributed uniformly throughout a sphere of radius 2R, the magnitude of the electric field at the same distance r1 from the center would be equal to
(Multiple Choice)
5.0/5  (47)
(47)
Showing 1 - 20 of 41
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)