Exam 9: Large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Numerical values of a test statistic for which 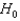 is not rejected:
is not rejected:
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
D
The owner of a marina would like to believe that more than 40% of the sailboat owners use their boats more than 6 times each summer. A random sample of 70 sailboat owners showed 42 used their boats more than 6 times each summer. Test the appropriate hypotheses using a significance level of 0.005. Is there reason for the marina owner to believe more than 40% of the sailboat owners use their boats more than 6 times each summer?
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Free
(Short Answer)
4.8/5  (34)
(34)
Correct Answer:
3.41; 2.575; reject H0; Yes, the marina owner is correct
A government testing agency studies aspirin capsules to see if customers are getting cheated with capsules that contain lesser amounts of medication than advertised. Suppose the testing agent concludes the capsules contain a mean amount below the advertised level when in fact the advertised level is the true mean. Which type of error, if any, did the testing agency commit?
(Multiple Choice)
4.9/5  (43)
(43)
If the probability of committing a Type I error for a given test is to be decreased, then for a fixed sample size n, which of the following statements is true?
(Multiple Choice)
4.7/5  (32)
(32)
In testing 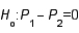 vs/
vs/ 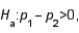 the following summary statistics are found:
the following summary statistics are found: 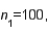
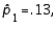
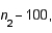 and
and 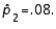 Based on these results, the null hypothesis should be rejected at the significance level
Based on these results, the null hypothesis should be rejected at the significance level 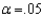 .
.
(True/False)
4.8/5  (32)
(32)
The public relations officer for a particular city claims the average monthly cost for childcare outside the home for a single child is $700. A potential resident is interested in whether the claim is correct. She obtains a random sample of 64 records and computes the average monthly cost of this type of childcare to be $689 with a standard deviation of $40.
Perform the appropriate test of hypothesis for the potential resident using 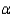 = 0.01.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Find the p-value for the test above.
p-value = ______________
What effect, if any, would there be on the conclusion in part (a) if you changed
= 0.01.
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
Interpretation: __________________________________________
Find the p-value for the test above.
p-value = ______________
What effect, if any, would there be on the conclusion in part (a) if you changed 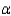 to 0.05?
The conclusion would ______________.
Find the power of the test when
to 0.05?
The conclusion would ______________.
Find the power of the test when 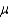 is actually $685 and
is actually $685 and 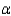 = 0.05.
______________
= 0.05.
______________
(Short Answer)
4.8/5  (30)
(30)
When the necessary conditions are met, a two-tail test is being conducted to test the difference between two population proportions. If the value of the test statistic is 2.05, then the p-value is:
(Multiple Choice)
4.7/5  (34)
(34)
When the necessary conditions are met, a two-tail test is being conducted to test the difference between two population means, but your statistical software provides only a one-tail area of 0.156 as part of its output. The p-value for this test will be 0.078.
(True/False)
4.9/5  (37)
(37)
If you wish to construct a confidence interval estimate for the difference between two population means, an increase in the sample sizes used will result in:
(Multiple Choice)
4.8/5  (41)
(41)
A sample of size 100 selected from one population has 60 successes, and a sample of size 150 selected from a second population has 95 successes. The test statistic for testing the equality of the population proportions equal to:
(Multiple Choice)
4.8/5  (43)
(43)
In testing 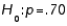 vs.
vs. 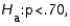 a random sample of size 100 produced a sample proportion
a random sample of size 100 produced a sample proportion 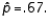 Given these results, the test statistic value is z = -.655.
Given these results, the test statistic value is z = -.655.
(True/False)
4.8/5  (32)
(32)
A proposition tentatively advanced as possibly true is called:
(Multiple Choice)
4.8/5  (39)
(39)
A large university claims that the average cost of housing within three miles of the campus is $6900 per school year. A high school student is preparing her budget for her freshman year at the university. She is concerned that the university's estimate is too low. Having taken AP Statistics, she decides to perform the following test of hypothesis: H0: 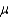 = 6900 versus Ha:
= 6900 versus Ha: 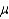 > 6900, where
> 6900, where 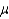 represents the average cost of housing per year within three miles of the university.
Describe the Type I error for this problem.
________________________________________________________
Describe the Type II error for this problem.
________________________________________________________
Which error has more serious consequences for the student?
________________________________________________________
represents the average cost of housing per year within three miles of the university.
Describe the Type I error for this problem.
________________________________________________________
Describe the Type II error for this problem.
________________________________________________________
Which error has more serious consequences for the student?
________________________________________________________
(Essay)
4.9/5  (22)
(22)
In testing the hypotheses H0: p1 - p2 = 0 vs. Ha: p1 - p2 > 0, use the following statistics, where x1 and x2 represent the number of defective components found in medical instruments in the two samples.
n1 = 200, x1 = 80
n2 = 400, x2 = 140
What conclusion can we draw at the 5% significance level?
Test statistic = ______________
Critical Value(s) = ______________
Conclusion: ______________
What is the p-value of the test?
p-value = ______________
Explain how to use the p-value to test the hypotheses.
____________________________
Estimate with 95% confidence the difference between the two population proportions.
______________
(Essay)
4.8/5  (34)
(34)
In hypothesis testing, the statement of the null hypothesis always contain the equality sign.
(True/False)
5.0/5  (38)
(38)
For testing the difference between two population proportions, the pooled proportion estimate should be used to compute the value of the test statistic when the:
(Multiple Choice)
4.9/5  (37)
(37)
In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 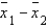 if the populations are normal with equal variances.
if the populations are normal with equal variances.
(True/False)
4.8/5  (37)
(37)
Hypothesis testing is a systematic approach to assessing tentative beliefs about reality, which involves confronting those beliefs with evidence and deciding, in light of this evidence, whether the beliefs can be maintained as reasonable or must be discarded as untenable.
(True/False)
4.9/5  (30)
(30)
A marketing manager wants to test the hypothesis that 90% of tennis magazine's subscribers live in their own homes. Accordingly, a simple random sample of 80 is taken from the magazine's list of subscribers. The sample turns out to contain 64 homeowners. Use a significance level of 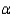 = .05.
Test statistic = ______________
p-value = ______________
Conclusion: ______________
Interpretation: __________________________________________
= .05.
Test statistic = ______________
p-value = ______________
Conclusion: ______________
Interpretation: __________________________________________
(Essay)
4.8/5  (34)
(34)
Showing 1 - 20 of 210
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)