Exam 5: Several Useful Discrete Distributions
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
The hypergeometric probability distribution formula calculates the probability of x successes when a random sample of size n is drawn without replacement from a population of size N within which M units have the characteristic that denotes success, and N - M units have the characteristic that denotes failure.
(True/False)
4.8/5  (33)
(33)
The Poisson probability distribution is an example of a continuous probability distribution.
(True/False)
4.9/5  (38)
(38)
In an effort to persuade customers to reduce their electricity consumption, special discounts have been offered for low consumption customers. In Florida, the EPA estimates that 70% of the residences have qualified for these discounts.
If we randomly select four residences in Florida, what is the probability exactly two of the four will have qualified for the discounts?
______________
If, instead, a sample of 20 residences is selected, what is the probability 12 or more will have qualified for the discounts?
______________
(Short Answer)
4.8/5  (36)
(36)
Let the random variable x have the Poisson distribution with mean 3.
What is the probability x will fall in the interval 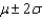 ?
______________
?
______________
(Short Answer)
4.8/5  (28)
(28)
An automobile service center can take care of 8 cars per day. Assume that the cars arrive at the service center randomly and independently of each other at a rate of 6 per hour, on average.
What is the standard deviation of the number of cars that arrive at the center?
______________
What is the probability of the service center being empty in any given hour?
______________
What is the probability that exactly 6 cars will be in the service center at any point during a given hour?
______________
What is the probability that less than 2 cars will be in the service center at any point during a given hour?
______________
(Short Answer)
4.8/5  (27)
(27)
Students arrive at a health center, according to a Poisson distribution, at a rate of 4 every 15 minutes. Let x represent number of students arriving in a 15 minute time period.
What is the probability that no more than 3 students arrive in a 15 minute time period?
______________
What is the probability that exactly 5 students arrive in a 15 minute time period?
______________
What is the probability that more than 5 students arrive in a 15-minute time period?
______________
What is the probability that between 4 and 8 students, inclusively, arrive in a 15-minute time period?
______________
(Short Answer)
4.8/5  (41)
(41)
Rebuilt ignition systems leave an aircraft repair shop at an average rate of 3 per hour. The assembly line needs four ignition systems in the next hour.
What is the probability they will be available?
______________
(Short Answer)
4.9/5  (23)
(23)
An applicant must score at least 80 points on a particular psychological test to be eligible for the Peace Corps. From nearly 30 years experience, it is known 60% of the applicants meet this requirement. Let the random variable x be the number of applicants who meet this requirement out of a (randomly selected) group of 25 applicants.
Find the mean of x.
______________
Find the standard deviation of x.
______________
Using the Empirical Rule, within what limits would you expect most (say, 95%) of the measurements to be?
________________________________________________________
(Essay)
4.8/5  (27)
(27)
The expected value, E(X), of a binomial probability distribution with n trials and probability p of success is:
(Multiple Choice)
4.9/5  (37)
(37)
An eight-cylinder automobile engine has two misfiring spark plugs. The mechanic removes all four plugs from one side of the engine.
What is the probability the two misfiring spark plugs are among those removed?
______________
What is the mean number of misfiring spark plugs?
______________
What is the variance of the number of misfiring spark plugs?
______________
(Short Answer)
4.8/5  (33)
(33)
The number of defects in a random sample of 200 parts produced by a machine is binomially distributed with p = .03. Based on this information, the expected number of defects in the sample is 6.
(True/False)
4.8/5  (42)
(42)
A telephone survey of American families is conducted to determine the number of children in the average American family. Past experience has shown that 30% of the families who are telephoned will refuse to respond to the survey. Which of the following statements is not a binomial random variable?
(Multiple Choice)
4.8/5  (36)
(36)
The probability the 1993-94 flu vaccine immunizes those receiving it is 0.97. If a random sample of 200 people receive the vaccine, what is the probability the vaccine will be ineffective on at most 5 people?
______________
(Short Answer)
5.0/5  (26)
(26)
Given that n is the number of trials and p is the probability of success in any one trial of a random experiment, the expected value of a binomial random variable equals:
(Multiple Choice)
4.7/5  (29)
(29)
The local Ford dealership claims 40% of their customers are return buyers, i.e., the customers previously purchased a Ford vehicle. Let the random variable x be the number of return buyers in a random sample of 10 recent customers.
Find 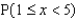 = ______________
Find P(x > 6) = ______________
What would you conclude about the accuracy of the dealership's claim if you found 9 repeat buyers in the sample? Explain your reasoning.
________________________________________________________
= ______________
Find P(x > 6) = ______________
What would you conclude about the accuracy of the dealership's claim if you found 9 repeat buyers in the sample? Explain your reasoning.
________________________________________________________
(Essay)
4.9/5  (28)
(28)
The number of teleport inquiries x in a timesharing computer system averages 0.2 per millisecond and follows a Poisson distribution.
Find the probability no inquiries are made during the next millisecond.
______________
Find the probability no inquiries are made during the next 3 milliseconds.
______________
(Short Answer)
4.8/5  (25)
(25)
The binomial distribution could be used to describe the spread of tennis balls when the players are serving.
(True/False)
4.8/5  (28)
(28)
Let x be a binomial random variable with n = 15 and p = 0.20.
Calculate P(x 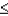 4) using the binomial formula.
______________
Calculate P(x
4) using the binomial formula.
______________
Calculate P(x 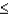 4) using the cumulative binomial probabilities table in Appendix I of your book.
______________
Are the results of your two previous answers very different, or very similar?
______________
Calculate the mean of the random variable x.
______________
Calculate the standard deviation of the random variable x.
______________
Fill in the table below:
4) using the cumulative binomial probabilities table in Appendix I of your book.
______________
Are the results of your two previous answers very different, or very similar?
______________
Calculate the mean of the random variable x.
______________
Calculate the standard deviation of the random variable x.
______________
Fill in the table below:
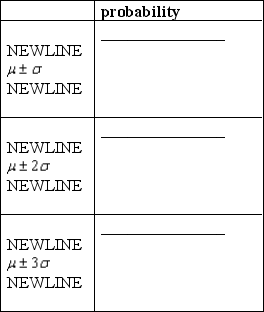 Are the results consistent with Tchebysheff's Theorem?
______________
With the Empirical Rule?
______________
Are the results consistent with Tchebysheff's Theorem?
______________
With the Empirical Rule?
______________
(Short Answer)
4.8/5  (37)
(37)
The binomial probability distribution is an example of discrete probability distributions.
(True/False)
4.9/5  (34)
(34)
Showing 101 - 120 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)