Exam 13: Multiple Regression Analysis
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Discuss some of the signals for the presence of multicollinearity.
Free
(Essay)
4.7/5  (39)
(39)
Correct Answer:
There are several clues to the presence of multicollinearity: a. An independent variable known to be an important predictor ends up having a partial regression coefficient that is not significant. b. A partial regression coefficient exhibits the wrong sign. c. When an independent variable is added or deleted, the partial regression coefficients for the other variables change dramatically. A more practical way to identify multicollinearity is through the examination of a correlation matrix, which is a matrix that shows the correlation of each variable with each of the other variables. A high correlation between two independent variables is an indication of multicollinearity.
Which of the following statements regarding multicollinearity is not true?
Free
(Multiple Choice)
4.9/5  (44)
(44)
Correct Answer:
C
A coefficient of multiple correlation is a measure of how well an estimated regression plane (or hyperplane) fits the sample data on which it is based.
Free
(True/False)
4.9/5  (28)
(28)
Correct Answer:
False
The stepwise regression analysis is best used as a preliminary tool for identifying which of a large number of variables should be considered in the model.
(True/False)
4.8/5  (38)
(38)
Stepwise regression is a statistical technique that is always implemented when developing a regression model to fit a nonlinear relationship between the dependent and potential independent variables.
(True/False)
4.8/5  (38)
(38)
If a stepwise regression procedure is used to enter, one at a time, three variables into a regression model, the resulting regression equation may differ from the regression equation that occurs when all three variables are entered at one step.
(True/False)
4.8/5  (38)
(38)
In regression analysis, a p-value provides the probability (judged by the t-value associated with an estimated regression coefficient) of 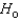 being true, given the claim
being true, given the claim 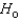 : The true regression coefficient equals 0.
: The true regression coefficient equals 0.
(True/False)
4.7/5  (33)
(33)
In a multiple regression model, which of the following statements is false?
(Multiple Choice)
4.8/5  (44)
(44)
A multiple regression analysis involving three independent variables and 25 data points results in a value of 0.769 for the unadjusted multiple coefficient of determination. Then, the adjusted multiple coefficient of determination is:
(Multiple Choice)
4.8/5  (34)
(34)
If multicollinearity exists among the independent variables included in a multiple regression model, then:
(Multiple Choice)
4.9/5  (32)
(32)
In a multiple regression analysis involving 24 data points, the mean squares for error, MSE, is 2, and the sum of squares for error, SSE, is 36. The number of the predictor variables must be:
(Multiple Choice)
4.9/5  (36)
(36)
Qualitative predictor variables are entered into a regression model through dummy variables.
(True/False)
4.9/5  (28)
(28)
In a multiple regression model, the coefficient of determination (sometimes called multiple 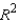 ) can be simply computed by squaring the largest correlation coefficient between the dependent variable, and any independent variable.
) can be simply computed by squaring the largest correlation coefficient between the dependent variable, and any independent variable.
(True/False)
4.7/5  (40)
(40)
The adjusted value of 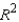 is mainly used to compare two or more regression models that have the same number of independent predictors to determine which one fits the data better.
is mainly used to compare two or more regression models that have the same number of independent predictors to determine which one fits the data better.
(True/False)
4.9/5  (31)
(31)
If we want to relate a random variable y to two-independent variables 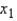 and
and 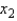 , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs.
, a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. 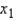 vs.
vs. 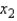 space and their associated multiple regression estimates, all of which lie on this hyperplane.
space and their associated multiple regression estimates, all of which lie on this hyperplane.
(True/False)
4.8/5  (36)
(36)
In testing the validity of a multiple regression model, a large value of the F-test statistic indicates that:
(Multiple Choice)
4.9/5  (33)
(33)
An engineer was investigating the relationship between the thrust of an experimental rocket (y), the percent composition of a secret chemical in the fuel (x1) and the internal temperature of a chamber of the rocket (x2). The engineer starts by fitting a quadratic model, but he believes that the full quadratic model is too complex and can be reduced by only including the linear terms and the interaction term.
The engineer obtained a random sample of 66 measurements and computed the SSE for both the complete model and the reduced model. The values were 1477.8 and 1678.8, respectively. Perform the appropriate test of hypothesis to determine whether the reduced model is adequate for the engineer's use. Use 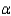 = 0.05.
Test statistic:
F = ______________
What is the critical value of F?
______________
Conclude:
______________
= 0.05.
Test statistic:
F = ______________
What is the critical value of F?
______________
Conclude:
______________  .
There ______________ evidence to indicate that at least one of the two quadratic variables is contributing significant information for predicting y.
.
There ______________ evidence to indicate that at least one of the two quadratic variables is contributing significant information for predicting y.
(Short Answer)
4.8/5  (37)
(37)
In a multiple regression analysis, if the model provides a poor fit, this indicates:
(Multiple Choice)
4.7/5  (26)
(26)
Showing 1 - 20 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)