Exam 5: Several Useful Discrete Distributions

Insulin-dependent diabetes (IDD) is a common chronic disorder of children. This disease occurs most frequently in persons of northern European descent. Let us assume that an area in Europe has an incidence of 6 cases per 100,000 per year. Can the distribution of the number of cases of IDD in this area be approximated by a Poisson distribution? ______________ What is the mean? ______________ What is the probability that the number of cases of IDD in this area is less than or equal to 3 per 100,000? ______________ What is the probability that the number of cases is greater than or equal to 3 but less than or equal to 7 per 100,000? ______________ Would you expect to observe 10 or more cases of IDD per 100,000 in this area in a given year? ______________ Why or why not? ________________________________________________________

A random sample of 4 units is taken from a group of 15 items in which 4 units are known to be defective. Assume that sampling occurs without replacement, and the random variable x represents the number of defective units found in the sample. The mean of the random variable x is: ______________ The variance of the random variable x is: ______________ P(x = 0) = ______________ P(x = 1) = ______________ P(x = 2) = ______________ P(x = 3) = ______________ P(x = 4) = ______________

The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is large.

The mean and variance of the Poisson distribution are equal.

A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that all four parts are from company B is approximately .008.

A Statistics Department is contacting alumni by telephone asking for donations to help fund a new computer laboratory. Past history shows that 80% of the alumni contacted in this manner will make a contribution of at least $50. A random sample of 20 alumni is selected. Let x represent number of alumni that makes at contribution of at least $50. What is the probability that exactly 15 alumni will make a contribution of at least $50? ______________ What is the probability that between 14 and 18 alumni, inclusively, will make a contribution of at least $50? ______________ What is the probability that less than 17 alumni will make a contribution of at least $50? ______________ What is the probability that more than 15 alumni will make a contribution of at least $50? ______________ How many alumni would you expect to make a contribution of at least $50? ______________

The hypergeometric probability distribution is used rather than the binomial distribution when the sampling is performed:

The number of telephone calls coming into a business' switchboard averages 4 calls per minute. Let x be the number of calls received. Find P(x = 0). ______________ What is the probability there will be at least one call in a given one-minute period? ______________ What is the probability at least one call will be received in a given two-minute period? ______________

A warehouse contains six parts made by company A and ten parts made by company B. If four parts are selected at random from the warehouse, the probability that none of the four parts is from company A is approximately .1154.

A college has seven applicants for three scholarships: four females and three males. Suppose that the seven applicants are equally qualified and that no preference is given by the selection committee for choosing either gender. Let x equal the number of female students chosen for the three scholarships. What is the mean of the distribution of x? ______________ What is the variance of the distribution of x? ______________ What is the probability that only one female will receive a scholarship? ______________ What is the probability that two females will receive a scholarship? ______________ What is the probability that none of the three males will receive a scholarship? ______________ What is the probability that none of the four females will receive a scholarship? ______________

The number of successes observed during the n trials of a binomial experiment is called the binomial random variable.

Suppose 40% of the TV sets in use in the U.S. on a particular night were tuned in to game 7 of the World Series. If we were to take a sample of six in-use TV sets that night, what is the probability exactly three are tuned to the World Series? ______________ If, instead, the sample consisted of 15 in-use TVs, what is the probability five or more are tuned to the World Series? ______________

From a group of 10 bank officers, 3 are selected at random to be relocated and supervise new branch offices. If two of the 10 officers are women and 8 are men, what is the probability exactly one of the officers to be relocated will be a woman? ______________

A warehouse contains 10 computer printers, 4 of which are defective. A company randomly selects five of the 10 printers to purchase. What is the probability all 5 are nondefective? ______________ What is the mean of x? ______________ What is the variance of x? ______________

The distribution of the number of phone calls to a doctor's office in a one-hour time period is likely to be described by a binomial distribution.

The Poisson probability distribution provides good approximations to binomial probabilities when n is large and 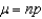is small, preferably with np < 7.

Which of the following distributions could not be used to describe the exact distribution for a continuous random variable?

The standard deviation of a binomial distribution for which n = 50 and p = 0.15 is:

A politician claims 55% of the voters will vote for him in an upcoming election. An independent watchdog organization queried a random sample of 500 likely voters, of whom only 249 said they would vote for the politician in question. Do the results of this sample support the politician's claim?

Which of the following statements is false with respect to a Poisson distribution?