Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Increasing the sample size n will result in a point estimate that is closer to the true value of the population parameter.
Free
(True/False)
4.9/5  (30)
(30)
Correct Answer:
False
The type of sample statistic that is used to make inferences about a given type of population parameter is called:
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
A
If the campaign manager of John Kerry is interested in estimating the proportion of registered voters who will support Kerry on November 2nd, 2004, the sample proportion 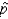 would be the appropriate point estimate.
would be the appropriate point estimate.
Free
(True/False)
4.7/5  (36)
(36)
Correct Answer:
True
A researcher wants to determine the proportion of elm trees in Superior, Wisconsin, dying of Dutch elm disease. Past experiments based on large sample sizes have shown this proportion to be 0.3. What sample size does the researcher need in order to estimate this proportion to within 0.04 with 95% confidence?
______________
(Short Answer)
4.8/5  (29)
(29)
An estimator is a random variable calculated from a random sample that provides either a point estimate or an interval estimate for some population parameter.
(True/False)
4.9/5  (29)
(29)
The term confidence interval refers to the range of values among which an unknown population parameter can presumably be found.
(True/False)
4.9/5  (40)
(40)
A study conducted by a commuter train transportation authority involved surveying a random sample of 200 passengers. The results show that a customer had to wait on the average 9.3 minutes with a standard deviation of 6.2 minutes to buy his or her ticket. Construct a 95% confidence interval for 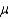 , the true mean waiting time.
______________
, the true mean waiting time.
______________
(Short Answer)
4.9/5  (30)
(30)
A childcare agency was interested in examining the amount that families pay per child per month for childcare outside the home. A random sample of 64 families was selected and the mean and standard deviation were computed to be $675 and $80, respectively.
Find a 95% confidence interval for the true average amount spent per child per month for childcare outside the home.
______________
Interpret the interval.
________________________________________________________
A social worker claims that the average amount spent per child per month outside the home is $700. Based on the interval above, can this claim be rejected?
______________
Justify your answer.
________________________________________________________
(Essay)
4.9/5  (31)
(31)
When estimating a population mean μ , where the population standard deviation σ is known, we can:
(Multiple Choice)
4.8/5  (39)
(39)
A random sample of 400 Michigan State University (MSU) students were surveyed recently to determine an estimate for the proportion of all MSU students who had attended at least three football games. The estimate revealed that between .372 and .458 of all MSU students attended. Given this information, we can determine that the confidence coefficient was approximately:
(Multiple Choice)
4.7/5  (40)
(40)
Suppose you wish to estimate a population proportion p based on sample of n observations. What sample size is required if you want your estimate to be within .03 of p with probability equal to 0.90?
(Multiple Choice)
4.9/5  (28)
(28)
The lower and upper limits of the 68.26% confidence interval for the population mean 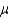 , given that n = 49;
, given that n = 49; 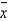 = 75; and
= 75; and 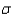 = 7, are 74 and 76, respectively.
= 7, are 74 and 76, respectively.
(True/False)
4.7/5  (34)
(34)
A 90% confidence interval estimate of the population mean 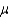 can be interpreted to mean that:
can be interpreted to mean that:
(Multiple Choice)
4.9/5  (44)
(44)
In developing an interval estimate for a population mean, a sample of 40 observations was used. The interval estimate was 17.25 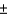 2.42. Had the sample size been 160 instead of 40, the interval estimate would have been:
2.42. Had the sample size been 160 instead of 40, the interval estimate would have been:
(Multiple Choice)
4.7/5  (37)
(37)
Whenever a sampled population is normally distributed or whenever the conditions of the central limit theorem are fulfilled, the sample mean, 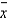 :
:
(Multiple Choice)
4.8/5  (31)
(31)
Suppose a 90% confidence interval for the mean time it takes to serve a customer at a drive-in bank is 120 seconds to 220 seconds. In repeated sampling 90% of the intervals constructed using the appropriate formula will contain the actual mean time.
(True/False)
4.9/5  (28)
(28)
Radio and television stations often air controversial issues during broadcast time and ask viewers to indicate their agreement or disagreement with a given stand on the issue. A poll is conducted by asking those viewers who agree to call a certain 900 telephone number and those who disagree to call a second 900 telephone number. All respondents pay a fee for their calls.
Does this polling technique result in a random sample?
______________
Are the results of such a survey valid?
______________
Explain.
________________________________________________________
(Essay)
4.9/5  (39)
(39)
If we wish to construct a 95% confidence interval estimate for the difference between two population proportions, then the confidence level would be:
(Multiple Choice)
4.9/5  (28)
(28)
A manufacturer wishes to estimate the mean time a battery pack will function before needing to be recharged with a margin of error of no more than 0.5 hours and with probability 0.95. If the standard deviation is known to be 1.5 hours, how many observations should be included in the sample?
______________
(Short Answer)
4.8/5  (39)
(39)
An auto mechanic knows the average time it takes to replace a bad car radiator is 70 minutes with a standard deviation of 12 minutes. This average is based on a random sample of 50. Construct a 90% confidence interval for 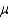 .
______________
.
______________
(Short Answer)
4.8/5  (26)
(26)
Showing 1 - 20 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)