Exam 2: A Preview of Calculus
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
A ring has a inner circumference of 10 centimeters. What is the radius of the ring? Round your answer to four decimal places.
(Multiple Choice)
5.0/5  (33)
(33)
Complete the table and use the result to estimate the limit.
x -10.1 -10.01 -10.001 -9.999 -9.99 -9.9 f(x)
(Multiple Choice)
4.8/5  (35)
(35)
Find the constant a such that the function
is continuous on the entire real line.
(Multiple Choice)
4.8/5  (27)
(27)
Determine the following limit. (Hint: Use the graph to calculate the limit.)
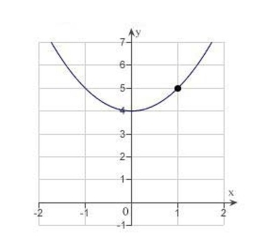
(Multiple Choice)
4.7/5  (44)
(44)
A 30 -foot ladder is leaning against a house (see figure). If the base of the ladder is pulled away from the house at a rate of 2 feet per second, the top will move down the wall at a rate of , where is the distance between the base of the ladder and the house. Find the rate when is 18 feet.
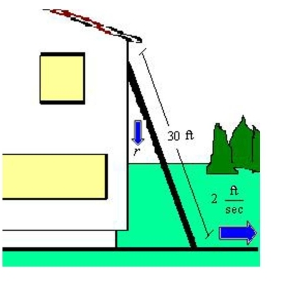
(Multiple Choice)
4.8/5  (40)
(40)
Find the value of c guaranteed by the Intermediate Value Theorem.
(Multiple Choice)
4.9/5  (42)
(42)
each additional minute or fraction thereof. Use the greatest integer function to write the cost of a call in terms of time (in minutes).
(Multiple Choice)
4.9/5  (43)
(43)
the rectangles in the following graph to approximate the area of the region bounded by , and .
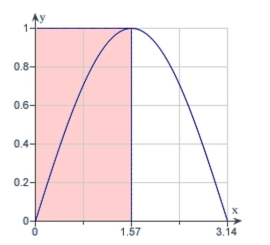
(Multiple Choice)
4.9/5  (26)
(26)
Find the constant such that the function
is continuous on the entire real line.
(Multiple Choice)
4.8/5  (40)
(40)
Find the slope of the secant line passing through and for . Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Showing 41 - 60 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)