Exam 7: Area of a Region Between Two Curves
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Use the shell method to find the volume of the solid generated by revolving the plane region bounded by
, about the line
(Multiple Choice)
4.8/5  (36)
(36)
where is measured in feet and corresponds to the center of the canal. Use the integration capabilities of a graphing utility to approximate the fluid force against a vertical gate used to stop the flow of water if the water is 3 feet deep. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the given lines.
(i) -axis;
(ii) the line
(Multiple Choice)
4.9/5  (23)
(23)
Set up and evaluate the integral that gives the volume of the solid formed by revolving the region bounded by , and about the -axis.
(Multiple Choice)
4.8/5  (38)
(38)
A force of 20 pounds stretches a spring 11 inches in an exercise machine. Find the work done in stretching the spring 2 feet from its natural position.
(Multiple Choice)
4.8/5  (33)
(33)
A cylindrical gasoline tank is placed so that the axis of the cylinder is horizontal. Find the fluid force on a circular end of the tank if the tank is half full, assuming that the diameter is Feet and the gasoline weighs 42 pounds per cubic foot.
(Multiple Choice)
4.7/5  (27)
(27)
Two electrons repel each other with a force that varies inversely as the square of the distance between them, where is the constant of proportionality. One electron is fixed at the point . Find the work done in moving the second electron from to .
(Multiple Choice)
4.7/5  (35)
(35)
Find the center of mass of the point masses lying on the x-axis. =7,=10,=8,=10,=8 =-9,=-2,=-6,=9,=6
(Multiple Choice)
4.7/5  (40)
(40)
A tank on the wing of a jet aircraft is formed by revolving the region bounded by the graph of and the -axis about the -axis, where and are measured in meters. Find the volume of the tank. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Use the disk or the shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the -axis.
(Multiple Choice)
4.8/5  (40)
(40)
Find the area of the region bounded by the graphs of the algebraic functions. f(x)=+30x+225 g(x)=17(x+15)
(Multiple Choice)
4.8/5  (38)
(38)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the line
(Multiple Choice)
4.8/5  (32)
(32)
Consider a beam of length the figure. In order to move a 550-pound object, a person weighing 214 pounds wants to balance it on the beam. Find x (the distance between the person and the fulcrum) such that the system is Equilibrium. Round your answer to two decimal places. 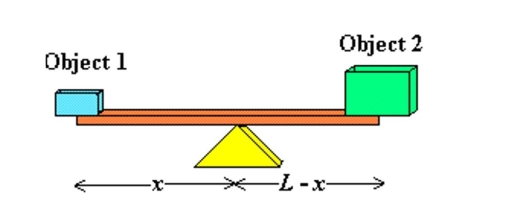
(Multiple Choice)
4.9/5  (45)
(45)
ِAn overhead garage door has two springs, one on each side of the door. A force of 12 pounds is required to stretch each spring 1 foot. Because of the pulley system, the springs stretch only One-half the distance the door travels. The door moves a total of 10 feet and springs are at their Natural length when the door is open. Find the work done by pair of strings.
(Multiple Choice)
4.8/5  (40)
(40)
Concrete sections for the new building have the dimensions (in meters) and shape as shown in the figure (the picture is not necessarily drawn to scale). Find the area of the face of the Section superimposed on the rectangular coordinate system. Round your answer to three decimal Places. 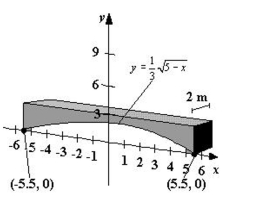
(Multiple Choice)
4.9/5  (38)
(38)
Find the center of mass of the point masses lying on the x-axis. =10,=1,=6,=5 =2,=-10,=-7,=-8
(Multiple Choice)
4.8/5  (39)
(39)
Find the center of mass of the given system of point masses. 8 8 8 7 9 , (5,-2) (6,-7) (2,4) (-7,-7) (-5,5)
(Multiple Choice)
4.8/5  (26)
(26)
Showing 61 - 80 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)