Exam 7: Area of a Region Between Two Curves
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Thr area of the top side of a piece of sheet metal is 9 square feet. The sheet metal is submerged horizontally in 8 feet of water. Find the fluid force on the top side. Round your answer to One decimal place.
(Multiple Choice)
4.8/5  (37)
(37)
A tank with a base of 4 feet by 3 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot. How much work is done in pumping water out over the top edge
In order to empty half of the tank. Round your answer to one decimal place. 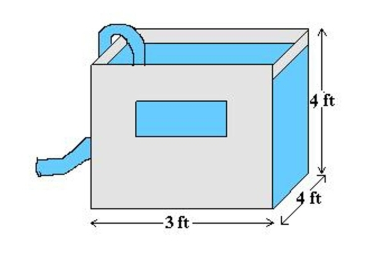
(Multiple Choice)
4.8/5  (30)
(30)
Find the center of mass of the given system of point masses. 10 1 9 3 , (-8,8) (1,8) (2,-10) (6,6)
(Multiple Choice)
4.9/5  (34)
(34)
Find the area of the region bounded by the graphs of the equations.
(Multiple Choice)
4.7/5  (29)
(29)
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a six-ton satellite to a height of 200 miles above earth. Assume that Earth has a radius of 4000 miles.
(Multiple Choice)
4.7/5  (32)
(32)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the line
(Multiple Choice)
4.9/5  (36)
(36)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis.
(Multiple Choice)
4.9/5  (39)
(39)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot.
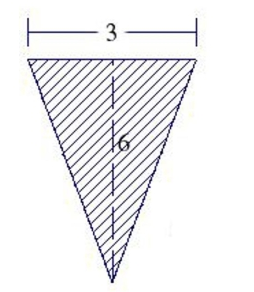
(Multiple Choice)
4.8/5  (26)
(26)
Use the shell method to set up and evaluate the integral volume of the solid generated by revolving the plane region about the y-axis.
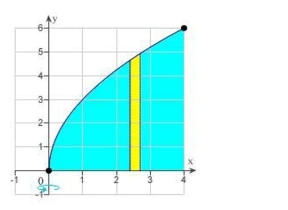
(Multiple Choice)
4.7/5  (34)
(34)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the y-axis.
(Multiple Choice)
4.8/5  (32)
(32)
Find the area of the surface generated by revolving the curve about the y-axis.
(Multiple Choice)
4.8/5  (27)
(27)
The figure is the vertical side of a form for poured concrete that weighs 140.7 pounds per cubic foot. Dimensions in the figure are in feet. Determine force on this part of the concrete form 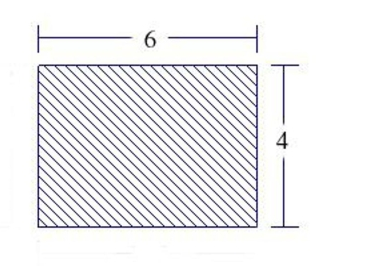
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the -axis. Verify your results using the integration capabilities of a Graphing utility.
(Multiple Choice)
5.0/5  (42)
(42)
Electrical wires suspended between two towers form a catenary modeled by the equation where and are measured in meters. The towers are 50 meters apart. Find the length of the suspended cable. Round your answer to three decimal places.
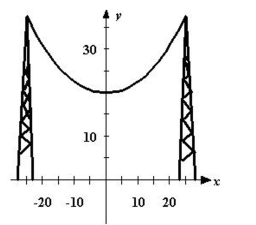
(Multiple Choice)
4.8/5  (34)
(34)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region bounded by about the -axis.
(Multiple Choice)
4.8/5  (36)
(36)
Use the disk or shell method to find the volume of the solid generated by revolving the region in the first quadrant bounded by the graph of the equation about the given line.
(i) the -axis; (ii) the -axis
(Multiple Choice)
4.8/5  (32)
(32)
A cylindrical gasoline tank 4 feet in diameter and 4 feet long is carried on the bank of a truck and is used to fuel tractors. The axis of the tank is horizontal. The opening on the tractor tank Is 5 feet above the top of the tank in the truck. Find the work done in pumping the entire gasoline
Contents that weighs 42 pounds per cubic feet of the fuel tank into a tractor. (Hint: Evaluate one Integral by geometric formula and the other by observing that the integrand is an odd function.)
(Multiple Choice)
4.7/5  (39)
(39)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations , and about the -axis. Round your answer to four decimal places.
(Multiple Choice)
4.7/5  (35)
(35)
about the -axis. A hole, centered along the axis of revolution, is drilled through this solid so that one-third of the volume is removed. Find the diameter of the hole. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Set up and evaluate the definite integral for the area of the surface formed by revolving the graph of about the -axis. Round your answer to three decimal places.
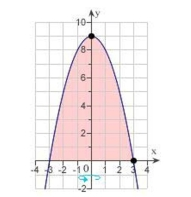
(Multiple Choice)
4.8/5  (33)
(33)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)