Exam 7: Area of a Region Between Two Curves
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the fluid force of a square vertical plate submerged in water, where meters and the weight-density of water is 9800 newtons per cubic meter. 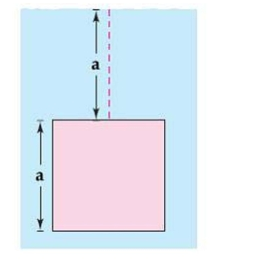
(Multiple Choice)
4.7/5  (34)
(34)
A porthole on a vertical side of a submarine (submerged in seawater) is . Find the fluid force on the porthole, assuming that the center of the square is feet below the surface.
(Multiple Choice)
4.9/5  (37)
(37)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the
(Multiple Choice)
4.8/5  (38)
(38)
as shown in the figure. Find if the parabola is tangent to the graph of . Round your answer to three decimal places.
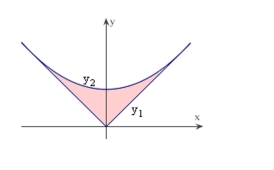
(Multiple Choice)
4.8/5  (40)
(40)
Find the area of the surface generated by revolving the curve about the x-axis.
(Multiple Choice)
5.0/5  (39)
(39)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region bounded by , and about the -axis. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations , and about the line .
(Multiple Choice)
4.8/5  (39)
(39)
Use the disk or the shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the line .
(Multiple Choice)
4.7/5  (37)
(37)
A tank on a water tower is a sphere of radius 65 feet. Determine the depth of the water when the tank is filled to one-fourth of its total capacity. (Note: Use the zero or root feature of a Graphing utility after evaluating the definite integral.) Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Find the fluid force on the vertical side of the tank, where the dimensions are given in feet. Assume that the tank is full of water. Note: The density of water is 62.4 lbs per cubic foot. 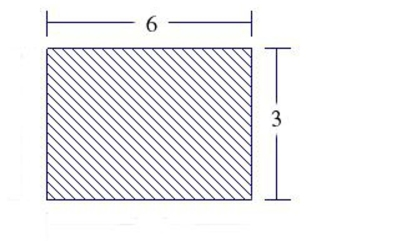
(Multiple Choice)
4.8/5  (24)
(24)
Find the area of the surface generated by revolving the curve about the y-axis.
(Multiple Choice)
4.7/5  (33)
(33)
Find the center of mass of the point masses lying on the x-axis. =10,=1,=7 =3,=10,=4
(Multiple Choice)
4.8/5  (28)
(28)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the line
(Multiple Choice)
4.8/5  (37)
(37)
A quantity of a gas with an initial volume of 1 cubic foot and a pressure of 2000 pounds per square foot expands to a volume of 7 cubic feet. Find the work done by the gas. Round Your answer to two decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
Concrete sections for the new building have the dimensions (in meters) and shape as shown in the figure (the picture is not necessarily drawn to scale). One cubic meter of concrete Weighs 4320 pounds. Find the weight of the section. Round your answer to the nearest pound. 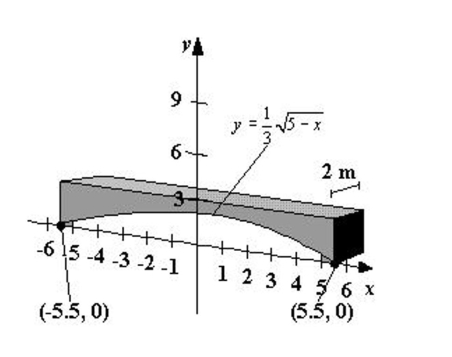
(Multiple Choice)
4.8/5  (35)
(35)
Find Mx, My, and ( , ) for the lamina of uniform density bounded by the graphs of the equations .
(Multiple Choice)
4.7/5  (35)
(35)
of dollars) for a large corporation. The model gives projected annual revenues from 2008 through 2015 , with corresponding to 2008 , and gives projected revenues if there is a decrease in the rate of growth of corporate sales over the period. Approximate the total reduction in revenue if corporate sales are actually closer to the model . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
in the figure. Two objects weighing 36 pounds and 108 pounds are placed at opposite ends of the beam. Find x (the distance between the fulcrum and the object weighing 36 pounds) such that the System is equilibrium. 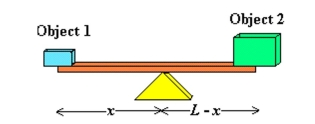
(Multiple Choice)
4.8/5  (35)
(35)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)