Exam 7: Area of a Region Between Two Curves
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
A solid is generated by revolving the region bounded by about the y-axis. A hole, centered along the axis of revolution, is drilled through this solid so that one-fourth of the volume is removed. Find the diameter of the hole. Round your answer
To three decimal places.
(Multiple Choice)
4.8/5  (36)
(36)
Use the Theorem of Pappus to find the volume of the solid formed by revolving the region bounded by the graphs of , and about the -axis. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
surface of a machine part is the region between the graphs of as shown in the figure. Find the area of the surface of the machine part. Round your answer to five decimal places.
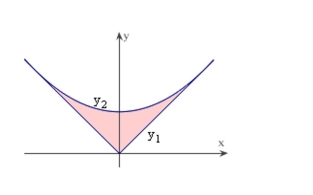
(Multiple Choice)
4.8/5  (33)
(33)
Find the center of mass of the given system of point masses. 9 4 7 , (-1,0) (7,-3) (1,-9)
(Multiple Choice)
4.8/5  (38)
(38)
Determine the work done by lifting a 140 pound bag of sugar 12 feet.
(Multiple Choice)
4.9/5  (37)
(37)
A cylindrical gasoline tank is placed so that the axis of the cylinder is horizontal. Find the fluid force on a circular end of the tank if the tank is full, assuming that the diameter is Feet and the gasoline weighs pounds per cubic foot. (Evaluate one integral by a geometric formula And the other by observing that the integrand is an odd function.) Round your answer to two decimal
Places.
(Multiple Choice)
4.7/5  (26)
(26)
A bridge has a main span of about 1400 meters. Each of its towers has a height of about 146 meters. Approximate the length of a parabolic cable along the main span if the length C of
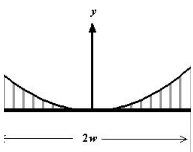
(Multiple Choice)
4.9/5  (45)
(45)
Set up and evaluate the definite integral for the area of the surface formed by revolving the graph of about the -axis.
(Multiple Choice)
4.8/5  (39)
(39)
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a 12-ton satellite to a height of 100 miles above Earth. Assume that the Earth has a Radius of 4000 miles.
(Multiple Choice)
5.0/5  (37)
(37)
Find the area of the region bounded by the graphs of the function . Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations , and about the line .
(Multiple Choice)
4.9/5  (35)
(35)
A force of 265 Newtons stretches a spring 20 centimeters. How much work is done in stretching the spring from 15 centimeters to 25 centimeters?
(Multiple Choice)
4.8/5  (36)
(36)
Set up the definite integral that gives the area of the region bounded by the graph of and
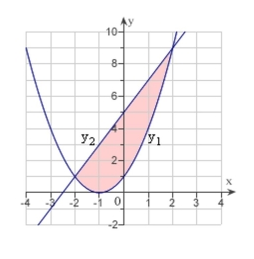
(Multiple Choice)
4.7/5  (33)
(33)
Find the fluid force of a triangular vertical plate submerged in water, where the dimensions are given in meters and the weight-density of water is 9800 newtons per cubic meter.
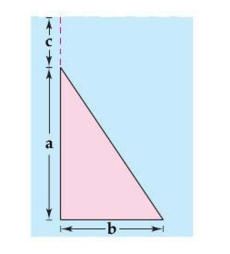
(Multiple Choice)
4.8/5  (24)
(24)
Use the integration capabilities of a graphing utility to approximate the arc length of the graph of . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)