Exam 13: Introduction to Functions of Several Variables
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
The average length of time that a customer waits in line for service is where is the average arrival rate, written as the number of customers per unit of time, and is the average service rate, written in the same units. Evaluate Note: and are given as the number of customers per hour.
(Multiple Choice)
4.9/5  (43)
(43)
Find least squares regression line for the points shown in the graph is Calculate S, the sum of the squared errors. 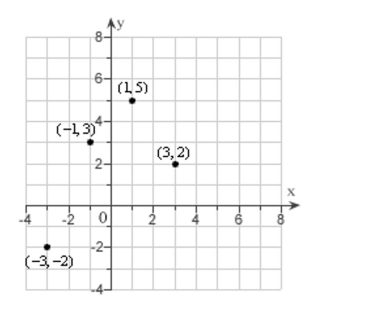
(Multiple Choice)
4.8/5  (46)
(46)
Describe the level curves of the function. Sketch the level curves for the given c-values.
(Multiple Choice)
5.0/5  (33)
(33)
Find the first partial derivative for the function respect to z.
(Multiple Choice)
5.0/5  (36)
(36)
Find the directional derivative of the function direction of . Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (41)
(41)
Suppose the temperature at any point where and are measured in meters. At the point find the rate of change of the temperature with respect to the distance moved along the plate in the direction of the -axis. Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (37)
(37)
Suppose electrical power P is given by resistance. Approximate the maximum percent error in calculating the power if 140 volts are applied to a 3000-ohm resistor and the possible percent errors in measuring E and R are 5% and 8%, Respectively.
(Multiple Choice)
4.9/5  (37)
(37)
Find the directional derivative of the function at P in the direction of
(Multiple Choice)
4.8/5  (32)
(32)
The radius r and height h of a right circular cylinder are measured with possible errors of 5% and 1%, respectively. Approximate the maximum possible percent error in measuring
The volume.
(Multiple Choice)
4.8/5  (35)
(35)
Determine whether there is a relative maximum, a relative minimum, a saddle point, or insufficient information to determine the nature of the function
(Multiple Choice)
4.9/5  (26)
(26)
Suppose a corporation manufactures candles at two locations. The cost of producing . The candles sell for per unit. Find the quantity that should be produced at each location to maximize the profit .
(Multiple Choice)
4.7/5  (31)
(31)
Find three positive numbers x, y, and z whose sum is 24 and product is a maximum.
(Multiple Choice)
4.8/5  (40)
(40)
Find the path of a heat-seeking particle placed at point with a temperature field .
(Multiple Choice)
4.8/5  (37)
(37)
Find the directional derivative of the function at P in the direction of
(Multiple Choice)
4.8/5  (30)
(30)
Showing 81 - 100 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)