Exam 15: Circuits Analysis in the S-Domain
Exam 1: Voltage, Current, Power, and Sources10 Questions
Exam 2: Circuit Laws10 Questions
Exam 3: Circuit Analysis Methods20 Questions
Exam 4: Circuit Theorems13 Questions
Exam 5: Operational Amplifier Circuits7 Questions
Exam 6: Capacitors and Inductors10 Questions
Exam 7: RL and RC Circuits14 Questions
Exam 8: RLC Circuits8 Questions
Exam 9: Phasors and Impedances8 Questions
Exam 10: Analysis of Phasor Transformed Circuits15 Questions
Exam 11: AC Power5 Questions
Exam 12: Three-Phase Systems6 Questions
Exam 13: Magnetically Coupled Circuits6 Questions
Exam 14: The Laplace Transform19 Questions
Exam 15: Circuits Analysis in the S-Domain26 Questions
Select questions type
Plot the magnitude and phase Bode diagrams of the transfer function given by
(Essay)
4.8/5  (26)
(26)
In the circuit shown below, let
Draw the circuit in the s-domain and find the Norton equivalent current and the Norton equivalent impedance . 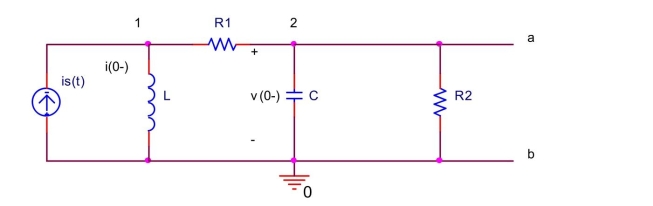
(Essay)
4.8/5  (31)
(31)
Plot the magnitude and phase Bode diagrams of the transfer function given by
(Essay)
4.8/5  (43)
(43)
In the circuit shown below, let
Draw the circuit in the s-domain and find the Thévenin equivalent voltage and the Thévenin equivalent impedance .
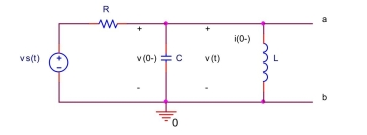
(Essay)
4.9/5  (35)
(35)
In the circuit shown below, let
Draw the circuit in the s-domain and find and for .
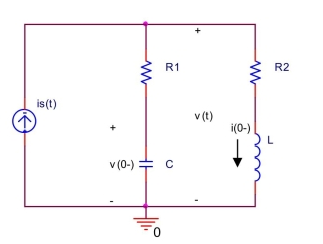
(Essay)
4.9/5  (31)
(31)
Showing 21 - 26 of 26
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)