Exam 18: Differential Forms and Exterior Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let 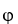 = 2dx + 5dy,
= 2dx + 5dy, 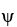 = -dx + 7dy and = -3dx + c dy be 1-forms on
= -dx + 7dy and = -3dx + c dy be 1-forms on 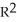 . Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11
. Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 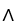 11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .
11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .
(Multiple Choice)
5.0/5  (36)
(36)
Let the differential 2-form 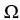 = (3
= (3 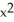 + 2xy + 6
+ 2xy + 6 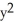 )dx
)dx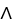 dy be defined in a star-like domain
dy be defined in a star-like domain 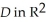 .
(a) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 closed?
(b) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 exact on D? If so, find a differential 1-form
.
(a) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 closed?
(b) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 exact on D? If so, find a differential 1-form 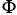 such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .
such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .
(Multiple Choice)
4.9/5  (45)
(45)
Find 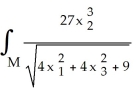 d
d  (x), where M is the 2-manifold in
(x), where M is the 2-manifold in 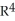 given parametrically by
given parametrically by 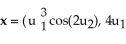 ,
, 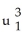 sin(2
sin(2 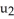 ), 3
), 3 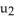 ) for 0 ≤
) for 0 ≤ 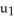 ≤ 1, 0 ≤
≤ 1, 0 ≤ 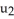 ≤ 1.
≤ 1.
(Short Answer)
4.8/5  (39)
(39)
Let M be the smooth 2-manifold 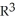 , x = p( ,
, x = p( , 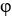 ) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let
) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let 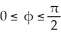 be a parametrization for M. If M is oriented by the differential 2-form
be a parametrization for M. If M is oriented by the differential 2-form 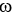 = zdx
= zdx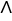 dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
(Short Answer)
4.9/5  (30)
(30)
Which of the following is an antiderivative of 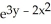 (3x + 4xy) dx
(3x + 4xy) dx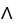 dy?
dy?
(Multiple Choice)
4.9/5  (40)
(40)
Let F(x, y) and G(x, y) be differential 0-forms on a domain D in 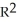 . Prove that(dF)∧(dG) =
. Prove that(dF)∧(dG) = 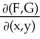 dx∧dy.
dx∧dy.
(Essay)
4.8/5  (34)
(34)
Let Ω be the differential 3-form 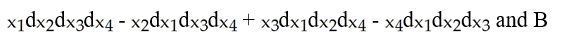 be the 4-dimensional ball of radius α in R4 ; that is
be the 4-dimensional ball of radius α in R4 ; that is
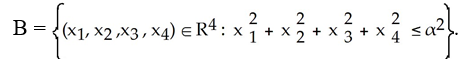 (a) Use the generalized Stokes's Theorem to evaluate
(a) Use the generalized Stokes's Theorem to evaluate 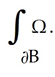 (b) Use part (a) to find the 4-volume of the ball.
Hint: You may use symmetry and the transformation , .
(b) Use part (a) to find the 4-volume of the ball.
Hint: You may use symmetry and the transformation , .
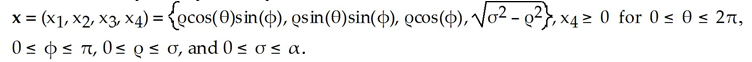
(Multiple Choice)
4.7/5  (38)
(38)
Let g(x) be a differential 0-form on a domain D in 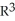 . If dg(x) =
. If dg(x) = 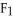 (x) dx+
(x) dx+ 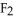 (x) dy +
(x) dy + 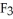 (x) dz, then the vector field
(x) dz, then the vector field 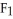 (x) i +
(x) i + 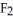 (x) j +
(x) j + 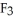 (x) k is equal to
(x) k is equal to
(Multiple Choice)
4.8/5  (42)
(42)
You probably know by now that a differential k-form k 1 on a domain D 
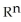 is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form
is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form 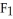 dx +
dx + 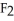 dy +
dy + 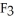 dz and the vector field F =
dz and the vector field F = 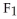 i +
i + 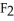 j +
j + 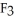 k. Using this setup, find the vector differential identity corresponding to the fact
k. Using this setup, find the vector differential identity corresponding to the fact 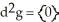 for any differential 0-form g on a domain D in
for any differential 0-form g on a domain D in 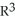 .
.
(Multiple Choice)
4.9/5  (28)
(28)
Let 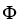 be a differential k-form and
be a differential k-form and 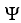 be a differential
be a differential 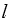 -form on a domain D
-form on a domain D 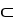
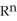 and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11
and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11 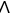 11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 )
11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 ) 
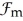 (D). Express m in terms of k and l.
(D). Express m in terms of k and l.
(Multiple Choice)
4.8/5  (44)
(44)
Evaluate the integral of 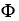 =
= 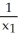 d
d 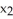
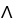 d
d 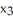 +
+ 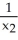 d
d 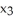 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 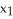 +
+ 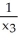 d
d 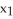 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 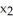 over the upper hemispherical surface
over the upper hemispherical surface 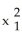 +
+ 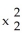 +
+ 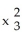 = 16,
= 16, 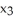 0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.
0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.
(Multiple Choice)
4.8/5  (40)
(40)
Find the 2-volume of the 2-manifold in 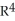 given parametrically by
given parametrically by 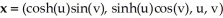 for 0 u 1, 0 v .
for 0 u 1, 0 v .
(Multiple Choice)
4.8/5  (34)
(34)
Let Φ = (2xy - 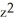 ) dx + (2yz +
) dx + (2yz + 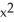 ) dy + (
) dy + ( 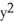 - 2zx) dz be a differential 1-form defined on a star-like domain D in
- 2zx) dz be a differential 1-form defined on a star-like domain D in 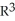 .
(a) Show that Φ is exact on D.
(b) Find a differential 0-form Ψsuch that Φ = dΨ on D.
.
(a) Show that Φ is exact on D.
(b) Find a differential 0-form Ψsuch that Φ = dΨ on D.
(Essay)
4.9/5  (37)
(37)
The 2-manifold M in R4 given by the equations 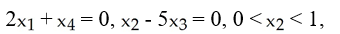 0 < x4 < 1,
0 < < 1 has normals
0 < x4 < 1,
0 < < 1 has normals 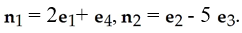 It is oriented by the 2-form
ω(x)( v1 , v2 ) = det( n1 n2 v1 v2 ). Let be a parametrization for M. Which of the following statements is true?
It is oriented by the 2-form
ω(x)( v1 , v2 ) = det( n1 n2 v1 v2 ). Let be a parametrization for M. Which of the following statements is true?
(Multiple Choice)
4.9/5  (43)
(43)
Let C be the curve of intersection of the cylinder 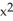 +
+ 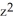 = 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate
= 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate 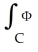 , where
, where 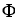 = -3
= -3 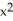 z dx + sin(y) dy + (3x
z dx + sin(y) dy + (3x 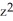 + x +7) dz.
+ x +7) dz.
(Multiple Choice)
4.7/5  (38)
(38)
Let 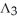 (
( 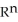 ) be the vector space of all 3-forms on
) be the vector space of all 3-forms on 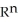 and
and 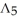 (
( 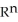 ) be the vector space of all 5-forms on
) be the vector space of all 5-forms on 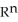 . If
. If 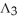 (
( 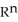 ) and
) and 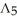 (
( 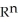 ) have the same dimension, find n.
) have the same dimension, find n.
(Multiple Choice)
4.9/5  (28)
(28)
Use the generalized Stokes's Theorem to find 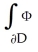 where
where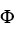 = 7x dy
= 7x dy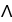 dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and
dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and 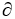 D is the oriented boundary of the conical domain D =
D is the oriented boundary of the conical domain D = 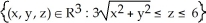 .
.
(Multiple Choice)
4.8/5  (40)
(40)
If 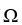 is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11
is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 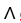 d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) =
d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) = 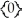 .
.
(True/False)
4.7/5  (36)
(36)
Showing 41 - 60 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)