Exam 18: Differential Forms and Exterior Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
You probably know by now that a differential k-form k 1 on a domain D 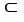
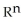 is very similar to a vector field on D, and hence a correspondence between the two may be established.Let
is very similar to a vector field on D, and hence a correspondence between the two may be established.Let 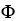 = F dx + G dy + H dz be a differential 1-form on a domain D
= F dx + G dy + H dz be a differential 1-form on a domain D 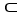
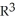 and let
and let 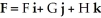 be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact
be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact 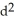 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 =
11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 = 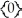 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Let S be a piece with boundary of a smooth 3-manifold in R4 (hypersurface) given by the equation 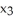 = g(
= g( 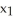 ,
, 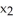 ,
, 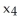 ) and let
) and let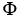 = d
= d 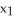
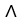 d
d 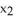 11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d
11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d 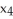 . Apart from sign due to orientation of S,
. Apart from sign due to orientation of S, 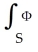 is equal to
is equal to
(Multiple Choice)
4.8/5  (34)
(34)
Let ![Let be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn( ) = -1.](https://storage.examlex.com/TB9661/11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11.jpg) be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
(True/False)
4.9/5  (37)
(37)
Calculate 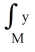 dx
dx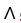 dz, where M is the surface given by z =
dz, where M is the surface given by z = 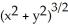 , 0 z 1, using the following parametrizations: (i) (x, y, z) = p(
, 0 z 1, using the following parametrizations: (i) (x, y, z) = p( 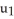 ,
, 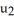 ) = (
) = ( 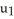 cos(
cos( 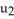 ),
), 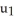 sin(
sin( 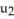 )
) 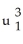 )
(ii) (x, y, z) = p(
)
(ii) (x, y, z) = p( 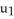 ,
, 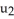 )= (
)= ( 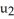 ,
, 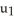 ,
, 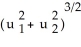 )
)
(Multiple Choice)
5.0/5  (28)
(28)
Let 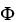 = xdx + vdv,
= xdx + vdv, 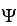 =
= 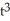 dy
dy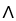 dw,
dw, 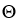 =
= 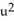 dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D
dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D 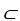
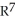 .Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11
.Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11 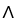 11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).
11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).
(Multiple Choice)
4.9/5  (45)
(45)
Let the differential 2-form 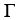 = xdy
= xdy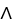 dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain
dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain 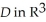 .
(a) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 closed?
(b) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 exact on D? If so, find a differential 1-form
.
(a) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 closed?
(b) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 exact on D? If so, find a differential 1-form 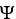 such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = d11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.
such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = d11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.
(Multiple Choice)
4.7/5  (40)
(40)
Let 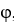 ,
, 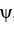 be differential 1-forms and let
be differential 1-forms and let 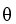 be a differential 0-form on
be a differential 0-form on 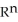 a domain D in Which of the following is a differential 2-form on D?
a domain D in Which of the following is a differential 2-form on D?
(Multiple Choice)
4.9/5  (34)
(34)
State the Divergence Theorem and Stokes's Theorem in 3-space, and Green's Theorem in 2-space in terms of differential forms.
(Essay)
4.7/5  (36)
(36)
Let 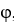 ,
, 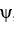 ,
, 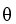 be 1-forms and
be 1-forms and 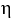 be a 2-form on
be a 2-form on 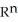 . Which of the following is a 3-form on
. Which of the following is a 3-form on 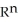 ?
?
(Multiple Choice)
4.7/5  (37)
(37)
Let ei , i = 1, 2, 3, 4 be the standard basis vectors in R4 and let 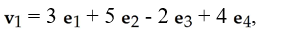
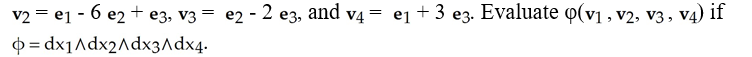
(Multiple Choice)
4.9/5  (37)
(37)
Find 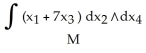 , where M is the 2-manifold in
, where M is the 2-manifold in 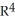 given parametrically by
given parametrically by 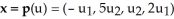 for 0 <
for 0 < 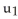 < 1, 0 <
< 1, 0 < 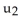 < 2.
< 2.
(Multiple Choice)
4.9/5  (43)
(43)
Find the 2-volume of the 2-parallelogram in 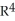 spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).
spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).
(Multiple Choice)
5.0/5  (32)
(32)
Let 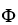 be a differential k-form and
be a differential k-form and 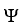 be a differential l-form on a domain D
be a differential l-form on a domain D 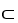
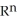 . State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11
. State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 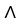 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.
11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.
(Multiple Choice)
4.9/5  (34)
(34)
Consider the unit cube Q = 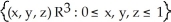 in
in 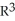 with the standard orientation given by
with the standard orientation given by 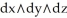 .Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in
.Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in 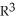 .
.
(Essay)
4.9/5  (38)
(38)
The k-volume of a k-parallelogram in 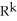 spanned by the k vectors,
spanned by the k vectors, 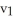 ,......,
,......, 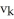
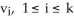 is given by det(A), where A is the k × k matrix whose columns are the components of the vectors.
is given by det(A), where A is the k × k matrix whose columns are the components of the vectors. 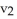
(True/False)
4.7/5  (30)
(30)
Showing 61 - 76 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)