Exam 9: Conics, Parametric Curves, and Polar Curves
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
What do the parametric equations x = t2 + 3t and y = t + 4 describe?
(Multiple Choice)
4.9/5  (27)
(27)
Find the area of the region bounded by the ellipse x = 7 cos
, y = 9 sin .
(Multiple Choice)
4.8/5  (32)
(32)
The graph of the rose curve r = cos(n ) has n leaves if n is an even integer and 2n leaves if n is an odd integer.
(True/False)
4.7/5  (34)
(34)
Find equations of the three normal lines to the parabola given parametrically by the equations
x(t) = 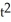 , y(t) = 2t, which pass through the point P (3, 0).
, y(t) = 2t, which pass through the point P (3, 0).
(Essay)
4.8/5  (38)
(38)
Find the points of intersection of the polar curves r = 4(1 + cos ) and r(1 - cos ) = 3.
(Multiple Choice)
4.7/5  (38)
(38)
Find the equation to the ellipse for which (1, -1) is a focus, x - y = 3 is the corresponding directrix, and the eccentricity is 1/2.
(Multiple Choice)
4.9/5  (32)
(32)
Determine the points where the parametric curve x = 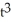 - 3t, y =
- 3t, y = 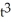 - 12t have horizontal and vertical tangents.
- 12t have horizontal and vertical tangents.
(Multiple Choice)
4.7/5  (33)
(33)
Find the equation of the tangent line to the curve at the given t. x = 2 cot t, y = 2 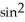 t at t =
t at t = 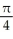
(Multiple Choice)
4.8/5  (31)
(31)
A plane curve C is given parametrically by x = tan(t) - 2, y = sec(t), t  (-
(- 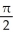 ,
, 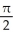 ).Find the Cartesian equation of the curve C.
).Find the Cartesian equation of the curve C.
(Multiple Choice)
4.8/5  (41)
(41)
Find the length of one arch of the cycloid x = a( - sin ), y = a(1 - cos ).
(Multiple Choice)
4.9/5  (35)
(35)
Find the area bounded by one petal of the flower r = a cos(5 ).
(Multiple Choice)
4.8/5  (31)
(31)
Find the slope of the curve x = 6t + 3, y = 2 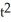 - 7t when t = 5.
- 7t when t = 5.
(Multiple Choice)
4.8/5  (34)
(34)
Find the length of the curve x = cos t + sin t, y = sin t - cos t, from t = 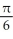 to t =
to t = 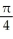 .
.
(Multiple Choice)
5.0/5  (40)
(40)
Find the equation of the tangent line to the curve at the given t. x = 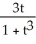 , y =
, y = 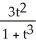 at t = 1.
at t = 1.
(Multiple Choice)
4.9/5  (38)
(38)
Find the area swept out by line segments from the origin to the curve r = tan from = 0 to = 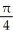 .
.
(Multiple Choice)
4.9/5  (40)
(40)
Describe the graph of the polar equation r = 6(sin + cos ).
(Multiple Choice)
4.8/5  (39)
(39)
Convert the polar equation r2 = sec(2 ) to Cartesian coordinates and identify the curve it represents.
(Multiple Choice)
4.8/5  (40)
(40)
Showing 21 - 40 of 114
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)