Exam 9: Conics, Parametric Curves, and Polar Curves

Find g(t) so that x = -1 + 3 cos(t), y = g(t), 0 $\le$ t $\le$ 2 $\pi$ provides a counterclockwise parametrization of the circle 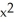+ + 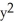2x - 4y = 4.

Find the arc length x = 2 cos $\theta$ + cos 2 $\theta$ + 1, y = 2 sin $\theta$ + sin 2 $\theta$ , for 0 $\le$ $\theta$$\le$ 2 $\pi$ .

Find the length of r = from $\theta$ = 0 to $\theta$ = 2 $\pi$ .

Find the Cartesian equation of the straight line tangent to the plane curve given parametrically by 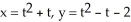at the point on the curve where t = -1.

The equation of a conic section in polar coordinates is given by r = 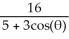.(i) Transform the equation of the conic section to rectangular coordinates (x , y).(ii) Identify the conic section.

Convert the point with Cartesian coordinates (-1, -1) to polar coordinates.

Find the equation of the parabola whose focus is (2, -1) and directrix is x + 2y -1 = 0.

The equations x(t) = 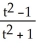, y(t) = 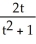, -1 $\le$ t $\le$ 1 are the parametric equations of

Find the area bounded by the polar curve r = sin(3 $\theta$ ).

A conic section is given by the equation 4x² + 10xy + 4y² = 36.Use rotation of coordinate axes through an appropriate acute angle $\theta$ to find the new equation of the conic section in the uv-coordinate axes , where x = u cos( $\theta$ ) - v sin( $\theta$ ) , y = u sin( $\theta$ ) + v cos( $\theta$ ). Then identify the conic section.

If x = f( $\theta$ ) cos( $\theta$ ), y = f( $\theta$ ) sin( $\theta$ ) for $\theta$ [ , ] , are parametric equations of a plane curve C, then the equation of curve C in polar coordinates is r = f( $\theta$ ), $\theta$ 1ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 [11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11 , 11ee7b18_ef83_6016_ae82_a1fef198316c_TB9661_11].

Express 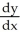and 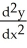in terms of x and y for the circle x = a cos $\theta$ , y = a sin $\theta$ .

Transform the polar equation r = 1 + 2 cos $\theta$ to rectangular coordinates.

Find the arc length of r = from $\theta$ = 0 to $\theta$ = .

Find an equation of a parabola satisfying the given conditions: Focus (2, 0) and directrix y = 2?.

For the parabola 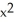+ 6x + 4y + 5 = 0, find the vertex, the focus, and the directrix.

Find the area bounded by the smaller loop of the curve r = 1 + 2 sin( $\theta$ ).

What are the polar coordinates of the highest point on the cardioid r = 2(1 + cos $\theta$ )?

Sketch the polar curve r = 4 sin(3θ).

Determine the coordinates of the points where the curve x = 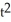+ 2t, y = 2 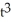+ 7 has (a) a horizontal tangent and (b) a vertical tangent.