Exam 5: More Applications of Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Use information from the function and its first two derivatives to sketch the graph of the function f(x) =  x -
x -  .
.
(Essay)
4.8/5  (38)
(38)
Find the absolute maximum and absolute minimum values of the function f(x) = 2 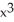 - 3
- 3 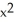 , -2 x 2.
, -2 x 2.
(Multiple Choice)
4.7/5  (34)
(34)
Find and classify all the local extrema of the function f(x) = x - sin2x.
(Multiple Choice)
4.7/5  (31)
(31)
A girl is on the bank of a river that is 1 kilometre wide. She wants to travel to a town on the opposite bank but 1 kilometre upstream. She intends to row in a straight line to some point P on the opposite bank and walk the remaining distance along the (straight) bank. To what point should she row in order to reach her destination in the least possible time if she can walk 5 kilometres per hour and row 3 kilometres per hour?Refer to the figure below:

(Multiple Choice)
4.7/5  (29)
(29)
Newton's Method with the initial approximation x1 = 1 is used to approximate the real root of the equation x3 + 3x - 1 = 0. Determine the value of x3, the third iteration of Newton's Method.
(Multiple Choice)
4.9/5  (40)
(40)
The function f(x) = 3x5 + Ax4 + Bx3 has inflection points at x = 0, x = -1, and x = 1. Find the values of the constants A and B.
(Multiple Choice)
4.9/5  (39)
(39)
Use information from the function and its first two derivatives to sketch the graph of the function 
(Essay)
4.8/5  (34)
(34)
Find the roots of the equation x3 - 5x - 3 = 0 correct to three decimal places using Newton's Method.
(Multiple Choice)
4.9/5  (36)
(36)
The graph shown in the figure below is the graph of which function?

(Multiple Choice)
4.8/5  (36)
(36)
A poster has an area of 800 cm2. An image is to be printed on the poster so that there are 4 cm margins at the top and bottom and 2 cm margins on either side. Find the maximum area such an image can have.
(Multiple Choice)
4.8/5  (31)
(31)
At a certain instant the length of one leg of a right triangle is 6 m and is increasing at 2 m/min while the length of the other leg is 8 m and is decreasing at 3 m/min. How fast is the area of the triangle changing at that instant?
(Multiple Choice)
4.9/5  (46)
(46)
Determine the concavity of f(x) = cos x + sin x on [0, 2π] and identify any points of inflection.
(Essay)
4.9/5  (42)
(42)
Find the ratio of the height h to the radius r of a cylindrical container having given volume V and having the least possible total surface area.
(Multiple Choice)
4.9/5  (25)
(25)
A balloon is 100 metres off the ground and rising vertically at the constant rate of 3 metres per second just as an automobile passes beneath it travelling along a straight, level road at the constant rate of 72 kilometres per hour. How fast is the distance between them changing one second later? (rounded to the nearest hundredth of a metre)
(Multiple Choice)
4.9/5  (47)
(47)
Determine the concavity of f(x) = 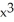 - 24
- 24 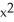 + 6x + 18 and identify any points of inflection.
+ 6x + 18 and identify any points of inflection.
(Multiple Choice)
4.8/5  (41)
(41)
Let P(x) be a polynomial in x, let k be a positive integer, and let 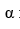 be a number such that
be a number such that 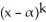 is a factor of
is a factor of 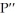 (x) but
(x) but 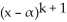 is not a factor of
is not a factor of 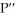 (x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?
(x). For what values of k is it possible that P(x) has a local maximum or minimum value at x = 11ee7b18_881f_7ad5_ae82_ef6a0704a9e3_TB9661_11?
(Multiple Choice)
4.8/5  (39)
(39)
Find the point (x, y) on the graph of y =  nearest the point (4, 0).
nearest the point (4, 0).
(Multiple Choice)
4.8/5  (28)
(28)
Showing 41 - 60 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)