Exam 5: More Applications of Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Let f(x) = 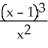 . Use information from f and its first two derivatives to sketch the graph of f.
. Use information from f and its first two derivatives to sketch the graph of f.
(Essay)
4.9/5  (40)
(40)
Find the height of the circular cylinder of maximum volume that will fit inside a sphere of radius R cm.
(Multiple Choice)
4.8/5  (39)
(39)
Find all inflection points of the graph of f(x) = 3 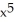 - 5
- 5 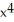 + 13x.
+ 13x.
(Multiple Choice)
4.9/5  (37)
(37)
Find all local extreme values of the function f(x) = 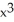 - 6
- 6 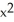 + 12x - 5 and their locations.
+ 12x - 5 and their locations.
(Multiple Choice)
4.7/5  (40)
(40)
Give the iteration formula for finding the roots of the equation sin x - x2 = 0 using Newton's Method.
(Multiple Choice)
4.7/5  (44)
(44)
Find the roots of the equation ln x - 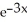 = 0 to four decimal places using Newton's Method.
= 0 to four decimal places using Newton's Method.
(Multiple Choice)
4.9/5  (33)
(33)
Find the inflection points of the graph of f(x) = 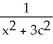 where c is a nonzero constant.
where c is a nonzero constant.
(Multiple Choice)
4.8/5  (40)
(40)
Given that 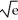 < 2, find an estimate for the size of the error if the Maclaurin polynomial of degree n for
< 2, find an estimate for the size of the error if the Maclaurin polynomial of degree n for 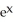 is used to approximate
is used to approximate 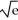 =
= 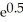 . How large need n be to ensure that this error is less than 10-4?
. How large need n be to ensure that this error is less than 10-4?
(Essay)
4.8/5  (39)
(39)
An aircraft is climbing at a 30-degree angle to the horizontal. How fast is the aircraft gaining altitude if its speed is 750 kilometres per hour?
(Multiple Choice)
5.0/5  (40)
(40)
The height of a right circular cylinder is increasing at the rate of 4 cm/s and its radius is decreasing at the rate of 2 cm/s. At what rate is the lateral surface area of the cylinder changing when the height is 3 centimetres and the radius is 1 centimetre?
The lateral surface area of a cylinder of base radius r and height h is given by S = 2 r h
(Multiple Choice)
4.8/5  (32)
(32)
Suppose Newton's Method applied to f(x) = 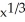 is used to "find"the root of the equation
is used to "find"the root of the equation 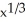 = 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
= 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
(Essay)
4.8/5  (38)
(38)
A plane is flying horizontally at an altitude of seven kilometres and a speed of 800 kilometres per hour. At time t = 0 the plane passes over a tracking station on the ground. How fast is the angle of elevation of the plane as measured at the tracking station changing 18 seconds later?
(Multiple Choice)
4.8/5  (37)
(37)
If f(x) is a polynomial of degree one and L(x) is the linearization of the function f about a, then f(x) = L(x).
(True/False)
4.9/5  (42)
(42)
Showing 61 - 80 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)