Exam 5: More Applications of Differentiation
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Given f(x) = 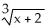 , c = -1, n = 2.
(i) Write out Taylor's Formula with Lagrange Remainder for the function f and the specified values of c and n.
(ii) Use part (i) to estimate the value of
, c = -1, n = 2.
(i) Write out Taylor's Formula with Lagrange Remainder for the function f and the specified values of c and n.
(ii) Use part (i) to estimate the value of 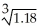 and estimate the error involved in the approximation.
and estimate the error involved in the approximation.
(Essay)
4.9/5  (36)
(36)
Find all local extreme values of the function f(x) = 2 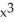 + 3
+ 3 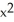 - 12x + 13 and their locations.
- 12x + 13 and their locations.
(Multiple Choice)
4.9/5  (42)
(42)
Find any extreme values and points of inflection of the function f(x) = x4 - 4 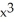 + 10.
+ 10.
(Multiple Choice)
4.9/5  (36)
(36)
Let g(x) = 3(x - 1)2/3 - x. Which of the following statements is true?
(Multiple Choice)
4.9/5  (41)
(41)
The function f(x) = 4 + k 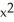 -
- 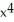 has a maximum value at x = 2. Find k.
has a maximum value at x = 2. Find k.
(Multiple Choice)
4.7/5  (32)
(32)
Determine the concavity of f(x) = cos x + sin x on [0, 2 ] and identify any points of inflection.
(Multiple Choice)
4.8/5  (34)
(34)
Which of the following statements best describes the graph of the function f(x) = 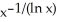 ?
?
(Multiple Choice)
4.9/5  (27)
(27)
A cylindrical can constructed from sheet metal holds a litre of oil. Find the radius of the can that will minimize the area of metal used to make the can. (Use 1 L = 1000 cm3.)
(Multiple Choice)
4.8/5  (37)
(37)
Find the area of the largest rectangle that can be inscribed in the ellipse 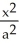 +
+ 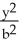 = 1.
= 1.
(Multiple Choice)
4.8/5  (44)
(44)
A lamp is 3 metres high on a post located 5 metres from a vertical wall. A 2 metre tall man walks toward the wall from the lamppost on a path perpendicular to the wall. He is walking at a rate of 1 metre per second. When he is 1 metre from the wall, how fast is the shadow of his head moving up the wall?
(Multiple Choice)
4.9/5  (32)
(32)
Find two nonnegative numbers whose sum is 9 such that the sum of one number and the square of the other number is a maximum.
(Multiple Choice)
4.8/5  (37)
(37)
Find the absolute maximum and absolute minimum values of the function f(x) = 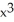 -
- 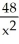 , -4 x -1.
, -4 x -1.
(Multiple Choice)
4.8/5  (52)
(52)
Use Newton's Method to find the x coordinate of a point on the curve y = x3 + 1 such that the tangent line to the curve at that point passes through the point (2, 0). Give your answer accurate to three decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
A water trough is 10 m long and has vertical cross-sections perpendicular to its long axis with the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height of 50 cm. If the trough is being filled with water at the rate of 0.2 cubic metres per minute, how fast is the water level rising when the water is 30 cm deep?
(Multiple Choice)
4.8/5  (39)
(39)
Let f(x) = 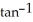 (x). Find the Taylor polynomial of f of degree 2 about c = 1.
(x). Find the Taylor polynomial of f of degree 2 about c = 1.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 81 - 100 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)