Exam 3: Functions and Graphs
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Give the equation of the horizontal asymptote of the rational function.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-A cereal factory has weekly fixed costs of . It costs to produce each box of cereal. A box of cereal sells for . Find the rule of the cost function that gives the total weekly cost of producing boxes of cereal.
(Multiple Choice)
4.9/5  (26)
(26)
Find the and intercepts. If no intercepts exist, state so.
-
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-Midtown Delivery Service delivers packages which cost per package to deliver. The fixed cost to run the delivery truck is per day. If the company charges per package, how many packages must be delivered daily to make a profit of ?
(Multiple Choice)
5.0/5  (34)
(34)
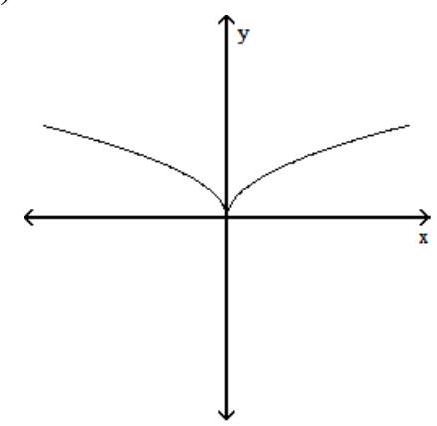
Use the vertical line test to determine if the graph is a graph of a function.
-
(True/False)
4.8/5  (37)
(37)
Write a cost function for the problem. Assume that the relationship is linear.
-Marginal cost, items cost to produce
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-Suppose the supply and demand for a certain videotape are given by:
Where is price and is quantity.
How many videotapes are demanded at a price of ?
(Multiple Choice)
4.9/5  (40)
(40)
Find the rule of a quadratic function whose graph has the given vertex and passes through the given point.
-vertex ; point
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-If a rock is thrown vertically upward from the surface of the moon at a speed of , its height after seconds will be meters. Find its height after 6 seconds.
(Multiple Choice)
4.9/5  (27)
(27)
Use a graphing calculator to find a viewing window that shows a complete graph of the given polynomial function(that is, a graph that includes all the peaks and valleys and indicates how the curve moves away frem the axis at thefar left and far right.) There are many possible correct answers.
-
(Essay)
4.8/5  (38)
(38)
Showing 161 - 180 of 323
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)