Exam 3: Functions and Graphs
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Give the equation of the vertical asymptote(s) of the rational function.
-
(Multiple Choice)
4.8/5  (33)
(33)
Solve the problem.
-Given the following revenue and cost functions, find the -value that makes profit a maximum. (Recall that profit equals revenue minus cost.)
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The graph of a function is given below. Tell whether the graph could possibly be the graph of a polynomial function. If it could be the graph of a polynomial function, tell which of the following are possible degrees for the polynomial function: 3, 4, 5, 6 .
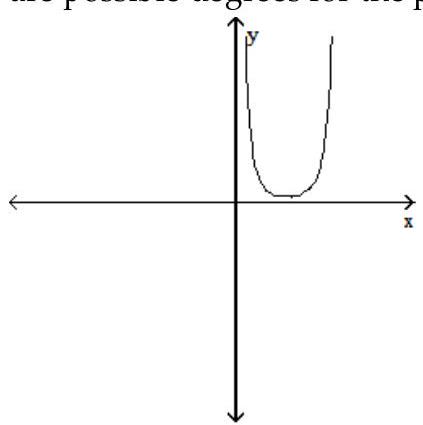
(Multiple Choice)
4.7/5  (40)
(40)
Use a graphing calculator to construct a table of values for the given function.
-Use a graphing calculator to display a table showing the (approximate) values of the function at .
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-At a manufacturing plant, the total cost (in dollars) to produce items is
.
What is the total cost to produce 2560 items?
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-John owns a hotdog stand. His profit is represented by the equation , with being profits and the number of hotdogs. What is the most he can earn?
(Multiple Choice)
4.9/5  (33)
(33)
Use the graph to solve the problem.
-In one city, the temperature in Fahrenheit on a typical summer day can be approximated by the following function:
Here, represents the number of hours since 6 a.m. The graph of this function is shown below. At what time does it start to get cooler?
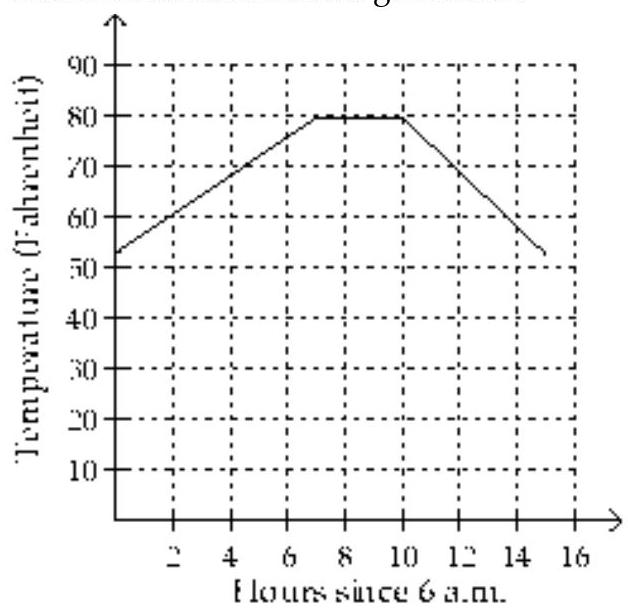
(Multiple Choice)
4.8/5  (32)
(32)
Solve the problem.
-A house was purchased for . After 6 years the value of the house was . Assume that the appreciation in value is given by a linear equation. Find the equation.
(Multiple Choice)
4.7/5  (29)
(29)
Solve the problem.
-The graph of a function is given below. Tell whether the graph could possibly be the graph of a polynomial function. If it could be the graph of a polynomial function, tell which of the following are possible degrees for the polynomial function: 3, 4, 5, 6 .
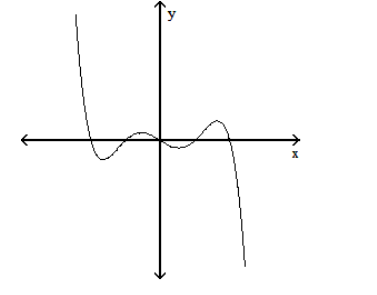
(Multiple Choice)
4.9/5  (40)
(40)
Find the appropriate linear cost or revenue function.
-Find the cost function given the following information. Fixed cost: ; marginal cost per item:
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem.
-Bob owns a watch repair shop. He has found that the weekly cost (in dollars) of operating his shop is given by
Where is the number of watches repaired. What is the cost of operating the shop if the number of watches repaired is 39 ?
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A lumber yard has fixed costs of a day and variable costs of per board - foot produced. The company gets per board-foot sold. How many board - feet must be produced daily to reach the break-even point?
(Multiple Choice)
4.9/5  (31)
(31)
Determine whether the following rule defines as a function of .
-
(True/False)
4.9/5  (38)
(38)
Showing 121 - 140 of 323
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)