Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the differential of the function at the indicated number. ;
(Short Answer)
4.8/5  (30)
(30)
Find the accumulated amount after 7 years on an investment of $2,000 earning an interest rate of 5% per year compounded continuously. Round to the nearest cent.
(Multiple Choice)
4.8/5  (44)
(44)
In calm waters, the oil spilling from the ruptured hull of a grounded tanker spreads in all directions. Assuming that the polluted area is circular, determine how fast the area is increasing when the radius of the circle is 20 ft and is increasing at the rate of ft/sec. Round to the nearest tenth if necessary.
(Short Answer)
4.8/5  (32)
(32)
Find the second derivative of the function.
h(t) = (t6 + 3) sin t
(Short Answer)
4.9/5  (33)
(33)
Two chemicals react to form another chemical. Suppose that the amount of chemical formed in time t (in hours) is given by where is measured in pounds.
a. Find the rate at which the chemical is formed when Round to two decimal places.
b. How many pounds of the chemical are formed eventually?
(Short Answer)
4.8/5  (42)
(42)
The displacement of a particle on a vibrating string is given by the equation where s is measured in centimeter and t in seconds. Find the velocity of the particle after t seconds.
(Short Answer)
4.8/5  (32)
(32)
Use implicit differentiation to find an equation of the tangent line to the curve at the given point.
(Multiple Choice)
5.0/5  (30)
(30)
Use the definition of the derivative to find the derivative of the function.
(Multiple Choice)
4.7/5  (38)
(38)
Two carts, A and B, are connected by a rope 39 ft long that passes over a pulley (see the figure below). The point Q is on the floor 12 ft directly beneath and between the carts. Cart A is being pulled away from Q at a speed of 2 ft/s. How fast is cart B moving toward Q at the instant when cart A is 5 ft from Q? 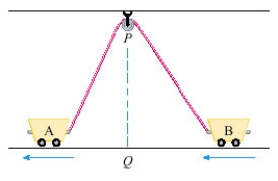
(Short Answer)
4.9/5  (35)
(35)
The position function of a body moving along a coordinate line is
s(t) = 3 sin t + 2 cos t
where t is measured in seconds and s(t) in feet. Find the position, velocity, speed, and acceleration of the body when t = .
(Short Answer)
4.7/5  (38)
(38)
If two resistors with resistances and are connected in parallel, as in the figure, then the total resistance measured in ohms ( ), is given by . If and are increasing at rates of and respectively, how fast is changing when and ?
Round the result to the nearest thousandth. 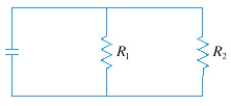
(Multiple Choice)
4.9/5  (32)
(32)
The function satisfies the hypotheses of the Mean Value Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem.
(Short Answer)
4.7/5  (40)
(40)
Showing 121 - 140 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)