Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Use logarithmic differentiation to find the derivative of the function.
(Multiple Choice)
4.8/5  (41)
(41)
Find equations of the tangent lines to the curve that are parallel to the line .
(Multiple Choice)
4.8/5  (27)
(27)
The mass of the part of a metal rod that lies between its left end and a point x meters to the right is . Find the linear density when x is 3 m.
(Multiple Choice)
4.8/5  (32)
(32)
Use the linear approximation of the function at to approximate the number .
(Multiple Choice)
4.9/5  (31)
(31)
The top of a ladder leaning against a wall is 8 ft above the ground. The slope of the ladder with respect to the ground is -4. What is the length of the ladder?
(Short Answer)
4.8/5  (38)
(38)
The equation of motion is given for a particle, where s is in meters and t is in seconds. Find the acceleration after seconds.
(Multiple Choice)
4.7/5  (41)
(41)
Water flows from a tank of constant cross-sectional area 50 through an orifice of constant cross-sectional area located at the bottom of the tank. Initially, the height of the water in the tank was 20 ft, and t sec later it was given by the equation How fast was the height of the water decreasing when its height was 2 ft? 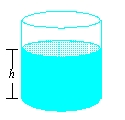
(Multiple Choice)
4.8/5  (35)
(35)
If a snowball melts so that its surface area decreases at a rate of , find the rate at which the diameter decreases when the diameter is 35 cm.
(Short Answer)
4.8/5  (36)
(36)
The quantity Q of charge in coulombs C that has passed through a point in a wire up to time t (measured in seconds) is given by . Find the current when .
(Multiple Choice)
4.9/5  (34)
(34)
Use logarithmic differentiation to find the derivative of the function.
(Short Answer)
4.7/5  (38)
(38)
In an adiabatic process (one in which no heat transfer takes place), the pressure P and volume V of an ideal gas such as oxygen satisfy the equation , where C is a constant. Suppose that at a certain instant of time, the volume of the gas is 2L, the pressure is 100 kPa, and the pressure is decreasing at the rate of 5 kPa/sec. Find the rate at which the volume is changing.
(Multiple Choice)
4.8/5  (45)
(45)
A boat is pulled into a dock by a rope attached to the bow of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. If the rope is pulled in at a rate of 1 m/s how fast is the boat approaching the dock when it is 7 m from the dock? Round the result to the nearest hundredth if necessary. 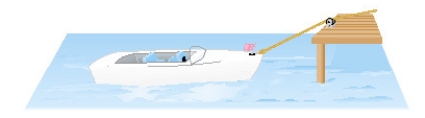
(Short Answer)
4.7/5  (38)
(38)
Find the equation of the tangent line to the given curve at the specified point.
(Short Answer)
4.8/5  (32)
(32)
Showing 141 - 155 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)