Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
y - x = x = cos y 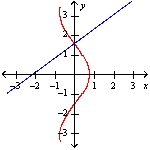
(Short Answer)
4.8/5  (35)
(35)
A spherical balloon is being inflated. Find the rate of increase of the surface area with respect to the radius r when r = 3 ft.
(Short Answer)
4.8/5  (43)
(43)
The mass of part of a wire is kilograms, where x is measured in meters from one end of the wire. Find the linear density of the wire when x = 16 m .
(Multiple Choice)
4.8/5  (40)
(40)
(a) Find the number c whose existence is guaranteed by the Mean Value Theorem for Integrals for the function f on [a, b], and (b) sketch the graph of f on [a, b] and the rectangle with base on [a, b] that has the same area as that of the region under the graph of
f. = + x; [0, 1]
(Short Answer)
4.9/5  (37)
(37)
Use logarithmic differentiation to find the derivative of the function.
(Multiple Choice)
4.8/5  (42)
(42)
Find the value of the expression accurate to four decimal places. sinh 4
(Multiple Choice)
4.8/5  (38)
(38)
Gravel is being dumped from a conveyor belt at a rate of 32 ft/min and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10 ft high? Round the result to the nearest hundredth. 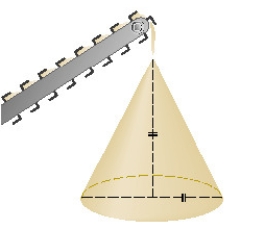
(Multiple Choice)
4.8/5  (41)
(41)
The height (in meters) of a projectile shot vertically upward from a point m above ground level with an initial velocity of 25.48 m/s is after t seconds.
a. When does the projectile reach its maximum height?
b. What is the maximum height?
(Multiple Choice)
4.8/5  (32)
(32)
The circumference of a sphere was measured to be 88 cm with a possible error of cm. Use differentials to estimate the maximum error in the calculated volume.
(Short Answer)
4.9/5  (40)
(40)
Showing 41 - 60 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)