Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The function satisfies the hypotheses of the Mean Value Theorem on the interval . Find all values of c that satisfy the conclusion of the theorem.
(Short Answer)
4.8/5  (36)
(36)
Find an equation of the tangent line to the curve at the point (4,1).
(Multiple Choice)
4.7/5  (31)
(31)
Determine the values of x for which the given linear approximation is accurate to within 0.07 at a = 0.
(Multiple Choice)
4.8/5  (36)
(36)
s(t) is the position of a body moving along a coordinate line, where , and s(t) is measured in feet and t in seconds.
a. Determine the time(s) and the position(s) when the body is stationary.
b. When is the body moving in the positive direction? In the negative direction?
c. Sketch a schematic showing the position of the body at any time t.
(Short Answer)
4.9/5  (34)
(34)
The altitude of a triangle is increasing at a rate of while the area of the triangle is increasing at a rate of . At what rate is the base of the triangle changing when the altitude is 10 cm and the area is .
(Short Answer)
4.9/5  (38)
(38)
Two sides of a triangle are 2 m and 3 m in length and the angle between them is increasing at a rate of rad/s. Find the rate at which the area of the triangle is increasing when the
Angle between the sides of fixed length is ( )
(Multiple Choice)
4.8/5  (41)
(41)
s(t) is the position of a body moving along a coordinate line; s(t) is measured in feet and t in seconds, where . Find the position, velocity, and speed of the body at the indicated time. ; t = 3
(Short Answer)
4.7/5  (36)
(36)
Find an equation of the tangent line to the curve at the point (4,1).
(Multiple Choice)
4.8/5  (32)
(32)
Find an equation of the tangent line to the given curve at the indicated point. 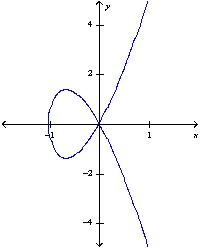
(Short Answer)
4.9/5  (29)
(29)
Showing 21 - 40 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)