Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find an equation of the tangent line to the graph of the function at the indicated point.
(Multiple Choice)
4.7/5  (31)
(31)
Find an equation of the line tangent to the graph of at the point where x = 0.
(Multiple Choice)
4.9/5  (44)
(44)
Find the point(s) on the graph of f where the tangent line is horizontal.
(Multiple Choice)
4.8/5  (27)
(27)
Use the table to estimate the value of
x 10 10.1 10.2 10.3 10.4 10.5 10.6 (x) 4.5 5.6 4.3 2.5 9.9 7.8 3.3 (x) 6.5 5.9 4.7 4.2 5.4 6.3 10
(Short Answer)
4.8/5  (40)
(40)
The curve with the equation is called an asteroid. Find an equation of the tangent to the curve at the point ( , 1). 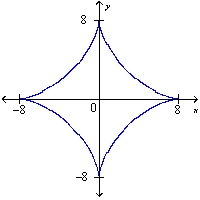
(Short Answer)
4.8/5  (45)
(45)
A mass on a spring vibrates horizontally on a smooth level surface (see the figure). Its equation of motion is , where t is in seconds and x in centimeters. Find the velocity at time t. 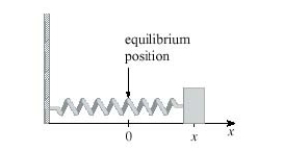
(Multiple Choice)
4.8/5  (42)
(42)
A telephone line hangs between two poles at 12 m apart in the shape of the catenary , where x and y are measured in meters. Find the slope of this curve where it meets the right pole. 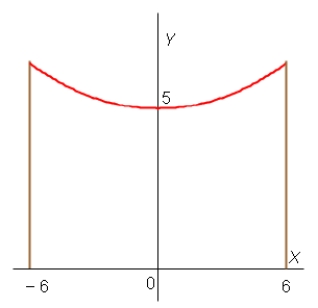
(Multiple Choice)
4.9/5  (39)
(39)
The parents of a child wish to establish a trust fund for the child's college education. If they need an estimated $90,000 5 years from now and they are able to invest the money at 5.5% compounded continuously in the interim, how much should they set aside in trust now?
(Multiple Choice)
4.7/5  (38)
(38)
Suppose that f and g are functions that are differentiable at x = 2 and that f (2) = -1, (2) = 3, g(2) = 3, and (2) = -4. Find .
(Short Answer)
4.8/5  (41)
(41)
Showing 61 - 80 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)