Exam 3: Applications of Differentiation
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
A turkey is removed from the oven when its temperature reaches and is placed on a table in a room where the temperature is . After 10 minutes the temperature of the turkey is and after 20 minutes it is . Use a linear approximation to predict the temperature of the turkey after minutes.
(Multiple Choice)
4.8/5  (44)
(44)
The position function of a particle is given by When does the particle reach a velocity of 1 m/s?
(Short Answer)
4.8/5  (43)
(43)
A body moves along a coordinate line in such a way that its position function at any time t is given by where is measured in feet and t in seconds. Find the velocity and acceleration of the body when .
(Short Answer)
4.8/5  (34)
(34)
If f is the focal length of a convex lens and an object is placed at a distance v from the lens, then its image will be at a distance u from the lens, where f ,v ,and u are related by the lens equation . Find the rate of change of v with respect to u.
(Multiple Choice)
4.9/5  (38)
(38)
A baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward first base with a speed of 32 ft/s. At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
(Short Answer)
4.9/5  (32)
(32)
The volume of a cube is increasing at a rate of . How fast is the surface area increasing when the length of an edge is .
(Short Answer)
4.9/5  (34)
(34)
Suppose the daily total cost (in dollars) of manufacturing x televisions is What is the marginal cost when x = 300? What is the actual cost incurred in manufacturing the 301st television?
(Multiple Choice)
4.9/5  (38)
(38)
Find the rate of change of y with respect of x at the indicated value of x. t = csc x - 18 cos x;
(Multiple Choice)
4.8/5  (33)
(33)
Find the points on the curve where the tangent is horizontal.
(Short Answer)
4.7/5  (39)
(39)
If two resistors with resistances and are connected in parallel, as in the figure, then the total resistance measured in ohms ( ), is given by . If and are increasing at rates of and respectively, how fast is changing when and ?
Round your answer to the nearest thousandth. 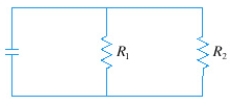
(Multiple Choice)
4.9/5  (40)
(40)
Find the equation of the tangent to the curve at the given point.
(Short Answer)
4.7/5  (33)
(33)
The top of a ladder slides down a vertical wall at a rate of m/s . At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s . How long is the ladder?
(Multiple Choice)
5.0/5  (26)
(26)
A plane flying horizontally at an altitude of 1 mi and a speed of mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station.
(Multiple Choice)
4.8/5  (34)
(34)
Showing 101 - 120 of 155
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)