Exam 13: Section 4: Functions of Several Variables
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Suppose a triangle is measured and two adjacent sides are found to be 5 inches and 7 inches long, with an included angle of 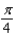 . The possible errors in measurement are
. The possible errors in measurement are 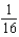 inch for the sides and 0.02 radian for the angle. Approximate the maximum possible error in the computation of the area. Round your answer to two decimal places.
inch for the sides and 0.02 radian for the angle. Approximate the maximum possible error in the computation of the area. Round your answer to two decimal places.
Free
(Multiple Choice)
4.8/5  (41)
(41)
Correct Answer:
B
Suppose the formula for wind chill C (in degrees Fahrenheit) is given by 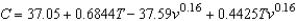 where v is the wind speed in miles per hour and T is the temperature in degrees Fahrenheit. The wind speed is
where v is the wind speed in miles per hour and T is the temperature in degrees Fahrenheit. The wind speed is  miles per hour and the temperature is
miles per hour and the temperature is 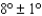 Fahrenheit. Use
Fahrenheit. Use 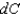 to estimate the relative error in calculating the wind chill. Round your answer to two decimal places.
to estimate the relative error in calculating the wind chill. Round your answer to two decimal places.
Free
(Multiple Choice)
5.0/5  (37)
(37)
Correct Answer:
E
Find the total differential for the function 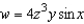 .
.
Free
(Multiple Choice)
4.8/5  (44)
(44)
Correct Answer:
E
Given 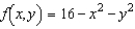 , use the total differential to approximate
, use the total differential to approximate 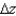 at
at 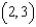 towards
towards 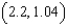 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (33)
(33)
Suppose the centripetal acceleration of a particle moving in a circle is 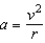 , where v is the velocity and r is the radius of the circle. Approximate the maximum percent error in measuring the acceleration due to errors of 4% in v and 2% in r.
, where v is the velocity and r is the radius of the circle. Approximate the maximum percent error in measuring the acceleration due to errors of 4% in v and 2% in r.
(Multiple Choice)
4.9/5  (37)
(37)
Find 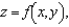 and use the total differential to approximate the quantity
and use the total differential to approximate the quantity 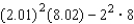 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Given 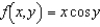 , use the total differential to approximate
, use the total differential to approximate 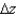 at
at 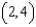 towards
towards 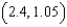 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (29)
(29)
Suppose the formula for wind chill C (in degrees Fahrenheit) is given by 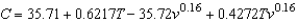 where v is the wind speed in miles per hour and T is the temperature in degrees Fahrenheit. The wind speed is
where v is the wind speed in miles per hour and T is the temperature in degrees Fahrenheit. The wind speed is 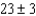 miles per hour and the temperature is
miles per hour and the temperature is 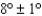 Fahrenheit. Use
Fahrenheit. Use 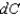 to estimate the maximum possible propagated error in calculating the wind chill. Round your answer to four decimal places.
to estimate the maximum possible propagated error in calculating the wind chill. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
Suppose electrical power P is given by 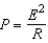 , where E is voltage and R is resistance. Approximate the maximum percent error in calculating the power if 140 volts are applied to a 3000-ohm resistor and the possible percent errors in measuring E and R are 5% and 8%, respectively.
, where E is voltage and R is resistance. Approximate the maximum percent error in calculating the power if 140 volts are applied to a 3000-ohm resistor and the possible percent errors in measuring E and R are 5% and 8%, respectively.
(Multiple Choice)
4.7/5  (35)
(35)
The radius r and height h of a right circular cylinder are measured with possible errors of 5% and 1%, respectively. Approximate the maximum possible percent error in measuring the volume.
(Multiple Choice)
4.8/5  (32)
(32)
Suppose the period T of a pendulum of length L is 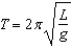 where g is the acceleration due to gravity. A pendulum is moved from the Canal Zone, where
where g is the acceleration due to gravity. A pendulum is moved from the Canal Zone, where 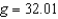 feet per second per second, to Greenland, where
feet per second per second, to Greenland, where 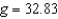 feet per second per second. Because of the change in temperature, the length of the pendulum changes from 2.6 feet to 2.45 feet. Approximate the change in the period of the pendulum. Round your answer to four decimal places.
feet per second per second. Because of the change in temperature, the length of the pendulum changes from 2.6 feet to 2.45 feet. Approximate the change in the period of the pendulum. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Given 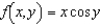 , calculate
, calculate 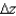 by evaluating
by evaluating 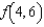 and
and 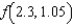 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
Given 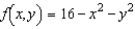 , calculate
, calculate 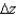 by evaluating
by evaluating 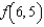 and
and 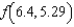 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.7/5  (43)
(43)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)