Exam 4: Section 7: Applications of Differentiation
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Find the point on the graph of the function 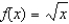 that is closest to the point
that is closest to the point 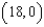 .
.
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
A
A sector with central angle 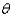 is cut from a circle of radius 10 inches, and the edges of the sector are brought together to form a cone. Find the magnitude of
is cut from a circle of radius 10 inches, and the edges of the sector are brought together to form a cone. Find the magnitude of 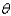 such that the volume of the cone is a maximum.
such that the volume of the cone is a maximum.
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Determine the dimensions of a rectangular solid (with a square base) with maximum volume if its surface area is 529 square meters.
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
D
A rectangle is bounded by the x- and y-axes and the graph of 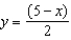 (see figure). What length and width should the rectangle have so that its area is a maximum?
(see figure). What length and width should the rectangle have so that its area is a maximum? 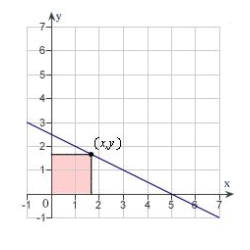
(Multiple Choice)
4.9/5  (28)
(28)
Find two positive numbers whose product is 181 and whose sum is a minimum.
(Multiple Choice)
4.7/5  (40)
(40)
On a given day, the flow rate F (cars per hour) on a congested roadway is given by 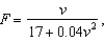 where v is the speed of the traffic in miles per hour. What speed will maximize the flow rate on the road? Round your answer to the nearest mile per hour.
where v is the speed of the traffic in miles per hour. What speed will maximize the flow rate on the road? Round your answer to the nearest mile per hour.
(Multiple Choice)
4.9/5  (38)
(38)
Find the point on the graph of the function 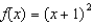 that is closest to the point
that is closest to the point 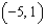 . Round all numerical values in your answer to four decimal places.
. Round all numerical values in your answer to four decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Assume that the amount of money deposited in a bank is proportional to the square of the interest rate the bank pays on this money. Furthermore, the bank can reinvest this money at 36%. Find the interest rate the bank should pay to maximize profit. (Use the simple interest formula.)
(Multiple Choice)
4.8/5  (38)
(38)
The sum of the perimeters of an equilateral triangle and a square is 19. Find the dimensions of the triangle and the square that produce a minimum total area.
(Multiple Choice)
4.8/5  (37)
(37)
A solid is formed by adjoining two hemispheres to the ends of a right circular cylinder. The total volume of the solid is 30 cubic centimeters. Find the radius, r, of the cylinder that produces the minimum surface area. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (25)
(25)
Find two positive numbers such that the sum of the first and twice the second is 56 and whose product is a maximum.
(Multiple Choice)
4.9/5  (30)
(30)
Find the length and width of a rectangle that has perimeter 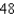 meters and a maximum area.
meters and a maximum area.
(Multiple Choice)
4.8/5  (37)
(37)
A Norman window is constructed by adjoining a semicircle to the top of an ordinary rectangular window (see figure). Find the dimensions of a Norman window of maximum area if the total perimeter is 38 feet. 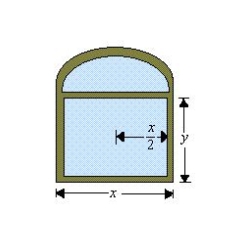
(Multiple Choice)
4.9/5  (36)
(36)
A rectangular page is to contain 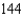 square inches of print. The margins on each side are 1 inch. Find the dimensions of the page such that the least amount of paper is used.
square inches of print. The margins on each side are 1 inch. Find the dimensions of the page such that the least amount of paper is used.
(Multiple Choice)
4.9/5  (30)
(30)
Find the length and width of a rectangle that has an area of 968 square feet and whose perimeter is a minimum.
(Multiple Choice)
4.8/5  (35)
(35)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)