Exam 11: Section 6: Vectors and the Geometry of Space
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Identify the following quadric surface. 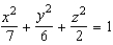
Free
(Multiple Choice)
4.8/5  (25)
(25)
Correct Answer:
E
Find the equation of the surface satisfying the conditions, and identify the surface. The set of points equidistant from the point (2, 4, 5 ) and the plane  .
.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
A
Identify the equation of the following graph. 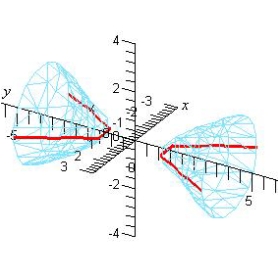
Free
(Multiple Choice)
4.8/5  (44)
(44)
Correct Answer:
E
Find an equation of the surface of revolution generated by revolving the curve given below in the indicated coordinate plane about the given axis. Equation of Curve
Coordinate Plane
Axis of Revolution 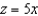
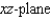
(Multiple Choice)
4.8/5  (43)
(43)
The top of a rubber bushing designed to absorb vibrations in an automobile is the surface of revolution generated by revolving the curve 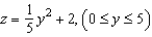 in the yz-plane about the z-axis. All measurements are in centimeters and the bushing is set on the xy-plane. Use the shell method to find its volume. Round your answer to one decimal place.
in the yz-plane about the z-axis. All measurements are in centimeters and the bushing is set on the xy-plane. Use the shell method to find its volume. Round your answer to one decimal place.
(Multiple Choice)
4.7/5  (27)
(27)
Given the equation of a surface of revolution 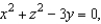 find the equation of its generating curve in the yz-plane rotating about the y-axis.
find the equation of its generating curve in the yz-plane rotating about the y-axis.
(Multiple Choice)
4.9/5  (37)
(37)
Some planet is an oblate ellipsoid rather than a sphere because of the forces caused by its rotation. The equatorial radius of this planet is 4739 miles and the polar radius is 4394 miles. Find the equation of the ellipsoid. (Assume that the center of a planet is at the origin and that the trace formed by the plane 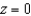 corresponds to the equator.)
corresponds to the equator.)
(Multiple Choice)
4.9/5  (42)
(42)
Find the length of the minor axis of the ellipse generated when the surface 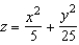 is intersected by the plane
is intersected by the plane 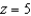 .
.
(Multiple Choice)
4.9/5  (33)
(33)
Find an equation for the surface of revolution generated by revolving the curve 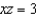 in the xz-plane about the z-axis.
in the xz-plane about the z-axis.
(Multiple Choice)
4.8/5  (29)
(29)
The top of a rubber bushing designed to absorb vibrations in an automobile is the surface of revolution generated by revolving the curve 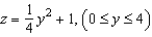 in the yz-plane about the z-axis. Find an equation for the surface of revolution.
in the yz-plane about the z-axis. Find an equation for the surface of revolution.
(Multiple Choice)
4.9/5  (30)
(30)
Find an equation of the surface of revolution generated by revolving the curve given below in the indicated coordinate plane about the given axis. Equation of Curve
Coordinate Plane
Axis of Revolution 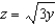
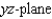
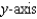
(Multiple Choice)
4.8/5  (37)
(37)
Use the shell method to find the volume of the solid below the surface formed by revolving the curve 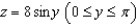 about the z-axis and above the xy-plane.
about the z-axis and above the xy-plane.
(Multiple Choice)
4.9/5  (32)
(32)
Find an equation of a generating curve given the equation of its surface of revolution. 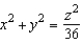 Equation of Curve Coordinate Plane
Axis of Revolution
Equation of Curve Coordinate Plane
Axis of Revolution
(Multiple Choice)
4.8/5  (30)
(30)
The top of a rubber bushing designed to absorb vibrations in an automobile is the surface of revolution generated by revolving the curve 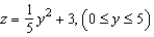 in the yz-plane about the z-axis. The bushing has a hole of 4 centimeters in diameter through its center and parallel to the axis of revolution. All measurements are in centimeters and the bushing is set on the xy-plane. Find the volume of the rubber bushing. Round your answer to two decimal places.
in the yz-plane about the z-axis. The bushing has a hole of 4 centimeters in diameter through its center and parallel to the axis of revolution. All measurements are in centimeters and the bushing is set on the xy-plane. Find the volume of the rubber bushing. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (39)
(39)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)