Exam 6: Section 2: Differential Equations
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
The half life of the radium isotope Ra-226 is approximately 1,599 years. If the amount left after 1,000 years is 1.8 g, what is the amount after 2000 years? Round your answer to three decimal places.
Free
(Multiple Choice)
4.7/5  (28)
(28)
Correct Answer:
A
The isotope 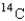 has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 1.2 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18000 years)? Round your answers to four decimal places.
has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 1.2 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18000 years)? Round your answers to four decimal places.
Free
(Multiple Choice)
4.7/5  (35)
(35)
Correct Answer:
C
Find the principal that must be invested at the rate 8%, compounded monthly, so that $1,000,000 will be available for retirement in 50 years. Round your answer to the nearest cent.
Free
(Multiple Choice)
5.0/5  (34)
(34)
Correct Answer:
B
The rate of change of N is proportional to N. When 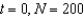 and when
and when 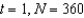 . What is the value of N when
. What is the value of N when 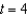 ? Round your answer to three decimal places.
? Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (27)
(27)
The isotope 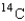 has a half-life of 5,715 years. Given an initial amount of 11 grams of the isotope, how many grams will remain after 500 years? After 5,000 years? Round your answers to four decimal places.
has a half-life of 5,715 years. Given an initial amount of 11 grams of the isotope, how many grams will remain after 500 years? After 5,000 years? Round your answers to four decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Write and solve the differential equation that models the following verbal statement: The rate of change of 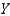 with respect to
with respect to 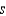 is proportional to
is proportional to 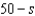 .
.
(Multiple Choice)
4.8/5  (27)
(27)
Find the function 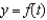 passing through the point
passing through the point 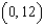 with the first derivative
with the first derivative 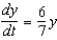 .
.
(Multiple Choice)
5.0/5  (36)
(36)
Find the time (in years) necessary for 1,000 to double if it is invested at a rate 6% compounded continuously. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (25)
(25)
The initial investment in a savings account in which interest is compounded continuously is $604. If the time required to double the amount is 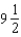 years, what is the amount after 15 years? Round your answer to the nearest cent.
years, what is the amount after 15 years? Round your answer to the nearest cent.
(Multiple Choice)
4.8/5  (42)
(42)
Find the function 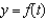 passing through the point
passing through the point 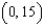 with the first derivative
with the first derivative 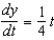 .
.
(Multiple Choice)
4.8/5  (31)
(31)
The initial investment in a savings account in which interest is compounded continuously is $813. If the time required to double the amount is 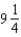 years, what is the annual rate? Round your answer to two decimal places.
years, what is the annual rate? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Suppose that the population (in millions) of Paraguay in 2007 was 6.7 and that the expected continuous annual rate of change of the population is 0.024. Find the exponential growth model 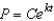 for the population by letting
for the population by letting 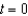 correspond to 2000. Round your answer to four decimal places.
correspond to 2000. Round your answer to four decimal places.
(Multiple Choice)
4.7/5  (36)
(36)
Suppose that the population (in millions) of a Egypt in 2007 is 80.3 and that expected continuous annual rate of change of the population is 0.017. The exponential growth model for the population by letting 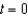 corresponds to 2000 is
corresponds to 2000 is 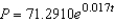 . Use the model to predict the population of the country in 2013. Round your answer to two decimal places.
. Use the model to predict the population of the country in 2013. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
The isotope 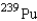 has a half-life of 24,100 years. After 10,000 years, a sample of the isotope is reduced 1.6 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 1,000 years? Round your answers to four decimal places.
has a half-life of 24,100 years. After 10,000 years, a sample of the isotope is reduced 1.6 grams. What was the initial size of the sample (in grams)? How large was the sample after the first 1,000 years? Round your answers to four decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
The half-life of the radium isotope Ra-226 is approximately 1,599 years. If the initial quantity of the isotope is 38 g, what is the amount left after 1,000 years? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
The number of bacteria in a culture is increasing according to the law of exponential growth. After 5 hours there are 175 bacteria in the culture and after 10 hours there are 425 bacteria in the culture. Answer the following questions, rounding numerical answers to four decimal places. (i) Find the initial population.
(ii) Write an exponential growth model for the bacteria population. Let t represent time in hours.
(iii) Use the model to determine the number of bacteria after 20 hours.
(iv) After how many hours will the bacteria count be 15,000?
(Multiple Choice)
4.8/5  (30)
(30)
Find the exponential function 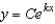 that passes through the two given points. Round your values of C and k to four decimal places.
that passes through the two given points. Round your values of C and k to four decimal places. 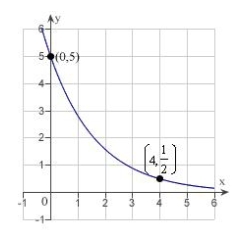
(Multiple Choice)
4.9/5  (34)
(34)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)