Exam 3: Section 8: Differentiation
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
Suppose that the total number of arrests T (in thousands) for all males ages 14 to 27 in 2006 is approximated by the model 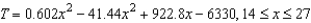 where x is the age in years (see figure). Approximate the two ages to one decimal place that had total arrests of
where x is the age in years (see figure). Approximate the two ages to one decimal place that had total arrests of 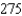 thousand.
thousand. 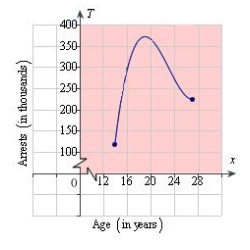
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
A
Use Newton´s Method to approximate the zero(s) of the function 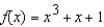 accurate to three decimal places.
accurate to three decimal places.
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
E
Approximate the fixed point of the function ![Approximate the fixed point of the function between to two decimal places. [A of a function f is a value of x such that .]](https://storage.examlex.com/TB4584/11eaa595_660a_69b5_a696_ad16604d32c7_TB4584_11_TB4584_11.jpg) between
between ![Approximate the fixed point of the function between to two decimal places. [A of a function f is a value of x such that .]](https://storage.examlex.com/TB4584/11eaa595_660a_69b6_a696_5385491cb3f7_TB4584_11_TB4584_11.jpg) to two decimal places. [A
to two decimal places. [A ![Approximate the fixed point of the function between to two decimal places. [A of a function f is a value of x such that .]](https://storage.examlex.com/TB4584/11eaa595_660a_90c7_a696_2f2139759300_TB4584_11_TB4584_11.jpg) of a function f is a value of x such that
of a function f is a value of x such that ![Approximate the fixed point of the function between to two decimal places. [A of a function f is a value of x such that .]](https://storage.examlex.com/TB4584/11eaa595_660a_90c8_a696_f112da3761d3_TB4584_11_TB4584_11.jpg) .]
.]
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
B
Complete two iterations of Newton's Method for the function 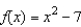 using the initial guess
using the initial guess 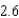 . Round your answers to four decimal places.
. Round your answers to four decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Use Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let ![Use Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6607_f89c_a696_cbb0176b9fa4_TB4584_11_TB4584_11.jpg) .]
.] ![Use Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6607_f89d_a696_dd29157046ad_TB4584_00_TB4584_00.jpg)
![Use Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6607_f89e_a696_55ae741fcc09_TB4584_00_TB4584_00.jpg)
![Use Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6608_1faf_a696_57a52513685c_TB4584_00_TB4584_00.jpg)
(Multiple Choice)
4.7/5  (38)
(38)
Use Newton's Method to approximate the zero(s) of the function 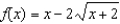 accurate to three decimal places.
accurate to three decimal places.
(Multiple Choice)
4.7/5  (42)
(42)
Use Newton's Method to approximate the zero(s) of the function 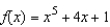 accurate to three decimal places.
accurate to three decimal places.
(Multiple Choice)
4.8/5  (35)
(35)
Complete two iterations of Newton's Method for the function 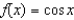 using the initial guess
using the initial guess 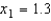 . Round all numerical values in your answer to four decimal places.
. Round all numerical values in your answer to four decimal places.
(Multiple Choice)
5.0/5  (44)
(44)
Approximate the positive zero(s) of the function 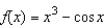 to three decimal places. Use Newton's Method and continue the process until two successive approximations differ by less than 0.001.
to three decimal places. Use Newton's Method and continue the process until two successive approximations differ by less than 0.001.
(Multiple Choice)
4.8/5  (38)
(38)
A manufacturer of digital audio players estimates that the profit for selling a particular model is 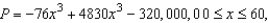 where P is the profit in dollars and x is the advertising expense in 10,000's of dollars (see figure). Find the smaller of two advertising amounts that yield a profit P of $
where P is the profit in dollars and x is the advertising expense in 10,000's of dollars (see figure). Find the smaller of two advertising amounts that yield a profit P of $ 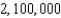 . Round your answer to the nearest dollar.
. Round your answer to the nearest dollar. 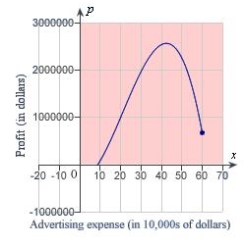
(Multiple Choice)
4.8/5  (41)
(41)
Use Newton's Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let ![Use Newton's Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6608_bbf5_a696_958c99954c2d_TB4584_11_TB4584_11.jpg) .]
.] ![Use Newton's Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6608_bbf6_a696_010ba5867d35_TB4584_11_TB4584_11.jpg)
![Use Newton's Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .]](https://storage.examlex.com/TB4584/11eaa595_6608_bbf7_a696_4bee90c14861_TB4584_00_TB4584_00.jpg)
(Multiple Choice)
4.9/5  (35)
(35)
Apply Newton's Method to approximate the x-value of the indicated point of intersection of ![Apply Newton's Method to approximate the x-value of the indicated point of intersection of Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .] Round your answer to three decimal places.](https://storage.examlex.com/TB4584/11eaa595_6609_7f4d_a696_bfb1bef59e1c_TB4584_11_TB4584_11.jpg) Continue the process until two successive approximations differ by less than 0.001. [Hint: Let
Continue the process until two successive approximations differ by less than 0.001. [Hint: Let ![Apply Newton's Method to approximate the x-value of the indicated point of intersection of Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .] Round your answer to three decimal places.](https://storage.examlex.com/TB4584/11eaa595_6609_7f4e_a696_875a52cc469f_TB4584_11_TB4584_11.jpg) .] Round your answer to three decimal places.
.] Round your answer to three decimal places. ![Apply Newton's Method to approximate the x-value of the indicated point of intersection of Continue the process until two successive approximations differ by less than 0.001. [Hint: Let .] Round your answer to three decimal places.](https://storage.examlex.com/TB4584/11eaa595_6609_a65f_a696_8df6267cc9c2_TB4584_00_TB4584_00.jpg)
(Multiple Choice)
4.9/5  (40)
(40)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)