Exam 12: Section 3: Vector-Valued Functions
Exam 1: Section 1: Preparation for Calculus16 Questions
Exam 1: Section 2: Preparation for Calculus26 Questions
Exam 1: Section 3: Preparation for Calculus23 Questions
Exam 1: Section 4: Preparation for Calculus16 Questions
Exam 1: Section 5: Preparation for Calculus25 Questions
Exam 1: Section 6: Preparation for Calculus8 Questions
Exam 2: Section 1: Limits and Their Properties10 Questions
Exam 2: Section 2: Limits and Their Properties14 Questions
Exam 2: Section 3: Limits and Their Properties25 Questions
Exam 2: Section 4: Limits and Their Properties20 Questions
Exam 2: Section 5 : Limits and Their Properties18 Questions
Exam 3: Section 1 : Differentiation20 Questions
Exam 3: Section 2: Differentiation25 Questions
Exam 3: Section 3: Differentiation26 Questions
Exam 3: Section 4 : Differentiation44 Questions
Exam 3: Section 5: Differentiation30 Questions
Exam 3: Section 6: Differentiation16 Questions
Exam 3: Section 7: Differentiation16 Questions
Exam 3: Section 8: Differentiation12 Questions
Exam 4: Section 1 : Applications of Differentiation19 Questions
Exam 4: Section 2: Applications of Differentiation17 Questions
Exam 4: Section 3: Applications of Differentiation17 Questions
Exam 4: Section 4: Applications of Differentiation26 Questions
Exam 4: Section 5: Applications of Differentiation23 Questions
Exam 4: Section 6: Applications of Differentiation22 Questions
Exam 4: Section 7: Applications of Differentiation15 Questions
Exam 4: Section 8: Applications of Differentiation16 Questions
Exam 4: Section 1: Integration19 Questions
Exam 4: Section 2: Integration17 Questions
Exam 4: Section 3: Integration19 Questions
Exam 4: Section 4: Integration18 Questions
Exam 4: Section 5: Integration31 Questions
Exam 4: Section 6: Integration18 Questions
Exam 4: Section 7: Integration27 Questions
Exam 4: Section 8: Integration16 Questions
Exam 4: Section 9: Integration20 Questions
Exam 6: Section 1: Differential Equations19 Questions
Exam 6: Section 2: Differential Equations25 Questions
Exam 6: Section 3: Differential Equations12 Questions
Exam 6: Section 4: Differential Equations14 Questions
Exam 6: Section 5: Differential Equations17 Questions
Exam 7: Section 1: Applications of Integration18 Questions
Exam 7: Section 2: Applications of Integration18 Questions
Exam 7: Section 3: Applications of Integration17 Questions
Exam 7: Section 4: Applications of Integration18 Questions
Exam 7: Section 5: Applications of Integration16 Questions
Exam 7: Section 6: Applications of Integration19 Questions
Exam 7: Section 7: Applications of Integration15 Questions
Exam 8: Section 1: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 2: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 3: Integration Techniques, Lhôpitals Rule, and Improper Integrals20 Questions
Exam 8: Section 4: Integration Techniques, Lhôpitals Rule, and Improper Integrals19 Questions
Exam 8: Section 5: Integration Techniques, Lhôpitals Rule, and Improper Integrals14 Questions
Exam 8: Section 6: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 8: Section 7: Integration Techniques, Lhôpitals Rule, and Improper Integrals18 Questions
Exam 8: Section 8: Integration Techniques, Lhôpitals Rule, and Improper Integrals15 Questions
Exam 9: Section 1: Infinite Series17 Questions
Exam 9: Section 2: Infinite Series23 Questions
Exam 9: Section 3: Infinite Series18 Questions
Exam 9: Section 4: Infinite Series21 Questions
Exam 9: Section 5: Infinite Series15 Questions
Exam 9: Section 6: Infinite Series21 Questions
Exam 9: Section 7: Infinite Series18 Questions
Exam 9: Section 8: Infinite Series18 Questions
Exam 9: Section 9: Infinite Series19 Questions
Exam 9: Section 10: Infinite Series16 Questions
Exam 10: Section 1: Conics, Parametric Equations, and Polar Coordinates26 Questions
Exam 10: Section 2: Conics, Parametric Equations, and Polar Coordinates17 Questions
Exam 10: Section 3: Conics, Parametric Equations, and Polar Coordinates22 Questions
Exam 10: Section 4: Conics, Parametric Equations, and Polar Coordinates15 Questions
Exam 10: Section 5: Conics, Parametric Equations, and Polar Coordinates18 Questions
Exam 10: Section 6: Conics, Parametric Equations, and Polar Coordinates19 Questions
Exam 11: Section 1: Vectors and the Geometry of Space20 Questions
Exam 11: Section 2: Vectors and the Geometry of Space21 Questions
Exam 11: Section 3: Vectors and the Geometry of Space18 Questions
Exam 11: Section 4: Vectors and the Geometry of Space18 Questions
Exam 11: Section 5: Vectors and the Geometry of Space21 Questions
Exam 11: Section 6: Vectors and the Geometry of Space20 Questions
Exam 11: Section 7: Vectors and the Geometry of Space19 Questions
Exam 12: Section 1: Vector-Valued Functions21 Questions
Exam 12: Section 2: Vector-Valued Functions24 Questions
Exam 12: Section 3: Vector-Valued Functions18 Questions
Exam 12: Section 4: Vector-Valued Functions20 Questions
Exam 12: Section 5: Vector-Valued Functions19 Questions
Exam 13: Section 1: Functions of Several Variables19 Questions
Exam 13: Section 2: Functions of Several Variables22 Questions
Exam 13: Section 3: Functions of Several Variables23 Questions
Exam 13: Section 4: Functions of Several Variables17 Questions
Exam 13: Section 6: Functions of Several Variables20 Questions
Exam 13: Section 7: Functions of Several Variables20 Questions
Exam 13: Section 8: Functions of Several Variables20 Questions
Exam 13: Section 9: Functions of Several Variables17 Questions
Exam 13: Section 10: Functions of Several Variables18 Questions
Exam 14: Section 1: Multiple Integration20 Questions
Exam 14: Section 2: Multiple Integration19 Questions
Exam 14: Section 3: Multiple Integration20 Questions
Exam 14: Section 4: Multiple Integration18 Questions
Exam 14: Section 5: Multiple Integration18 Questions
Exam 14: Section 6: Multiple Integration19 Questions
Exam 14: Section 7: Multiple Integration19 Questions
Exam 14: Section 8: Multiple Integration19 Questions
Exam 15: Section 1: Vector Analysis21 Questions
Exam 15: Section 2: Vector Analysis18 Questions
Exam 15: Section 3: Vector Analysis18 Questions
Exam 15: Section 4: Vector Analysis18 Questions
Exam 15: Section 5: Vector Analysis21 Questions
Exam 15: Section 6: Vector Analysis18 Questions
Exam 15: Section 7: Vector Analysis18 Questions
Exam 15: Section 8: Vector Analysis17 Questions
Select questions type
The quarterback of a football team releases a pass at a height of 8 feet above the playing field, and the football is caught by a receiver 38 yards directly downfield at a height of 4 feet. The pass is released at an angle of 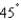 with the horizontal. Find the speed of the football when it is released. Round your answer to three decimal places.
with the horizontal. Find the speed of the football when it is released. Round your answer to three decimal places.
Free
(Multiple Choice)
4.7/5  (40)
(40)
Correct Answer:
B
The quarterback of a football team releases a pass at a height of 8 feet above the playing field, and the football is caught by a receiver 46 yards directly downfield at a height of 4 feet. The pass is released at an angle of 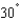 with the horizontal. Find the time in seconds the receiver has to reach the proper position after the quarterback releases the football. Round your answer to one decimal place.
with the horizontal. Find the time in seconds the receiver has to reach the proper position after the quarterback releases the football. Round your answer to one decimal place.
Free
(Multiple Choice)
4.9/5  (42)
(42)
Correct Answer:
B
The position vector 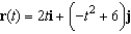 describes the path of an object moving in the xy-plane. Sketch a graph of the path and sketch the velocity and acceleration vectors at the point
describes the path of an object moving in the xy-plane. Sketch a graph of the path and sketch the velocity and acceleration vectors at the point 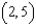 .
.
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
C
The position vector 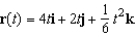 describes the path of an object moving in space. Find the acceleration
describes the path of an object moving in space. Find the acceleration 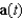 of the object.
of the object.
(Multiple Choice)
4.7/5  (38)
(38)
Determine the maximum height of a projectile fired at a height of 6 feet above the ground with an initial velocity of 700 feet per second and at an angle of 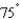 above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Use the given acceleration function and initial conditions to find the position at time t = 1. 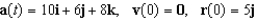
(Multiple Choice)
4.7/5  (30)
(30)
The position vector 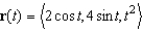 describes the path of an object moving in space. Find the velocity
describes the path of an object moving in space. Find the velocity 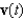 of the object.
of the object.
(Multiple Choice)
4.8/5  (36)
(36)
A baseball, hit 9 feet above the ground, leaves the bat at an angle of 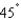 and is caught by an outfielder 9 feet above the ground and 500 feet from home plate. What is the initial speed of the ball? Round your answer to two decimal places.
and is caught by an outfielder 9 feet above the ground and 500 feet from home plate. What is the initial speed of the ball? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
The position vector 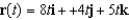 describes the path of an object moving in space. Find the speed
describes the path of an object moving in space. Find the speed 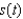 of the object.
of the object.
(Multiple Choice)
4.9/5  (34)
(34)
Determine the range of a projectile fired at a height of 5 feet above the ground with an initial velocity of 1000 feet per second and at an angle of 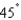 above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
above the horizontal. Use the model for projectile motion, assuming there is no air resistance. Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Find the vector-valued function for the path of a projectile launched at a height of 20 feet above the ground with an initial velocity of 50 feet per second at an angle of 35 degrees above the horizontal. Use a graphing utility to graph the path of the projectile and confirm your selection. Let i be the unit vector in the horizontal direction and j the unit vector in the vertical direction.
(Multiple Choice)
4.9/5  (36)
(36)
Use the given acceleration function and initial conditions to find the position at time t = 1. 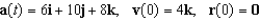
(Multiple Choice)
4.7/5  (36)
(36)
The position vector 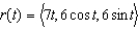 describes the path of an object moving in space. Find the speed
describes the path of an object moving in space. Find the speed 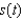 of the object.
of the object.
(Multiple Choice)
4.8/5  (31)
(31)
The quarterback of a football team releases a pass at a height of 6 feet above the playing field, and the football is caught by a receiver 76 yards directly downfield at a height of 2 feet. The pass is released at an angle of 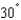 with the horizontal. Find the maximum height of the football. Round your answer to one decimal place.
with the horizontal. Find the maximum height of the football. Round your answer to one decimal place.
(Multiple Choice)
4.8/5  (37)
(37)
A baseball, hit 5 feet above the ground, leaves the bat at an angle of 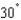 and its caught by an outfielder 5 feet above the ground and 500 feet from home plate. How high does the ball rise? Round your answer to the nearest integer.
and its caught by an outfielder 5 feet above the ground and 500 feet from home plate. How high does the ball rise? Round your answer to the nearest integer.
(Multiple Choice)
4.8/5  (38)
(38)
A baseball player at second base throws a ball 87 feet to the player at first base. The ball is thrown 5 feet above the ground with an initial velocity of 50 miles per hour and at an angle of 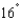 above the horizontal. At which height does the player at first base catch the ball? Round your answer to three decimal places.
above the horizontal. At which height does the player at first base catch the ball? Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (43)
(43)
The position vector 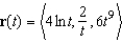 describes the path of an object moving in space. Find the velocity
describes the path of an object moving in space. Find the velocity 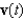 of the object.
of the object.
(Multiple Choice)
4.7/5  (38)
(38)
Use the given acceleration function and initial conditions to find the position at time t = 3. 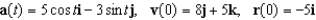
(Multiple Choice)
4.9/5  (31)
(31)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)