Question 1

Which of the following is a solution of the differential equation $\frac { d ^ { 2 } y } { d x ^ { 2 } } + 4 y = 0$

Accepted Answer

A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$ 
A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$

Question 2

When a child was born, her grandparents placed $1000 in a savings account at 10% interest compounded continuously, to be withdrawn at age 20 to help pay for college. How much money is in the account at the time of withdrawal?

Accepted Answer

A)  $1000 e$ 
B)  $500 e$ 
C)  $500 e ^ { 2 }$ 
D)  $2000 e ^ { 2 }$ 
E)  $4000 e$ 
F) $2000 e$ 
G) $1000 e ^ { 2 }$ 
H) $4000 e ^ { 2 }$ 
A)  $1000 e$ 
B)  $500 e$ 
C)  $500 e ^ { 2 }$ 
D)  $2000 e ^ { 2 }$ 
E)  $4000 e$ 
F) $2000 e$ 
G) $1000 e ^ { 2 }$ 
H) $4000 e ^ { 2 }$

Question 3

Find the solution to the differential equation $\frac { d y } { d x } = e ^ { x - y }$ that satisfies the initial condition $y ( 0 ) = 1$ .

Accepted Answer

The answer of Find the solution to the differential equation...

Question 4

$2000 is invested at 5% annual interest. Find the value of A(t) at the end of t years if:
(a) the interest compounds monthly.(b) the interest compounds continuously.

Accepted Answer

The answer of $2000 is invested at 5% annual interest....

Question 5

Which of the following equations is satisfied by the function $x = e ^ { 2 t ^ { 2 } }$ ?

Accepted Answer

A)  $x ^ { \prime } - 2 t = 0$ 
B)  $x ^ { \prime } - 4 x t = 0$ 
C)  $x ^ { \prime \prime } + 4 x = 0$ 
D)  $x ^ { \prime \prime } + x = 0$ 
E)  $x ^ { \prime } - 4 x = 0$ 
F) $x ^ { \prime } + 4 x = 0$ 
G) $x ^ { \prime \prime } - 4 x = 0$ 
H) $x ^ { \prime \prime } - x = 0$ 
A)  $x ^ { \prime } - 2 t = 0$ 
B)  $x ^ { \prime } - 4 x t = 0$ 
C)  $x ^ { \prime \prime } + 4 x = 0$ 
D)  $x ^ { \prime \prime } + x = 0$ 
E)  $x ^ { \prime } - 4 x = 0$ 
F) $x ^ { \prime } + 4 x = 0$ 
G) $x ^ { \prime \prime } - 4 x = 0$ 
H) $x ^ { \prime \prime } - x = 0$

Question 6

The study of free fall provides one context to consider differential equations. In the simplest case, in the absence of air or other resistance, physicists assume that the rate of change of velocity of a body is constant. But it is more realistic to consider the presence of air resistance. Assume that $g$ is the constant of acceleration due to earth's gravity. Suppose that air resistance is proportional to the velocity of the falling body.(a) Explain why the differential equation $\frac { d v } { d t } = g - k v$ , where $k$ is a positive constant, would be a reasonable model for velocity under these conditions.
(b) When does $\mathcal { V }$ increase most rapidly? Justify your answer.
(c) Consider the equation in part (a). What would happen to the rate of change of velocity, $\frac { d v } { d t }$ , as $t$ increases? Justify your conclusion.
(d) Make a sketch of a possible solution for this differential equation.

Accepted Answer

(a) @#IMG-DLM& shows that the ratio at which the v

Question 7

(a) What can you conclude about the functions which satisfy $y ^ { \prime } = y ^ { 2 }$ just by looking at the differential equation?
(b) Verify that $y = - \frac { 1 } { x + c }$ are solutions of the equation in part (a).
(c) Is there a solution of the equation in part (a) that is not a member of the family of functions in part (b)? Justify your answer.
(d) Find a solution to the equation in part (a) with the additional condition that $y ( 0 ) = \frac { 1 } { 3 }$ .

Accepted Answer

(a) @#IMG-DLM& is a constant solution an

Question 8

The half-life of Carbon 14 is 5700 years. A wooden table is measured with 80% of Carbon 14 compared with newly cut tree. Find the age of the table.

Accepted Answer

A) 2, 933 years 
B) 1,000 years 
C) 500 years 
D) 2,000 years 
E) 13,235 years
F)4,200 years
G)1,835 years
H)3,000 years 
A) 2, 933 years 
B) 1,000 years 
C) 500 years 
D) 2,000 years 
E) 13,235 years
F)4,200 years
G)1,835 years
H)3,000 years

Question 9

Consider the following predator-prey system where x and y are in millions of creatures and t represents time in years: $\begin{array} { l } 
\frac { d x } { d t } = 2 x - x y \
\frac { d y } { d t } = - 4 y + x y
\end{array}$ 
(a) Show that (4, 2) is the nonzero equilibrium solution.
(b) Find an expression for $\frac { d y } { d x }$ .
(c) The direction field for the differential equation is given below: 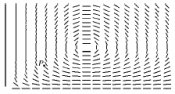  (i) Locate (4, 2) on the graph.(ii) Sketch a rough phase trajectory through P indicated in the graph.(d) With the aid of the phase trajectory, answer the following questions:
(i) For the region \(0  4 and 0  4 and y > 2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(iv) For the region 0  2, is x (t) increasing or decreasing? Is y (t) increasing or decreasing? Describe in words how the two species interact with one another.(e) Suggest a pair of species which might interact in the manner described by this system.

Accepted Answer

(a) Solve the system of equations @#IMG-DLM& (b) @#IMG-DLM&

Question 10

Carbon 14, with a half-life of 5700 years, is used to estimate the age of organic materials. What fraction of the original amount of carbon 14 would an object have if it were 2000 years old?

Accepted Answer

A)  $e ^ { - ( 57 / 20 ) \ln 2 }$ 
B)  $\frac { 57 } { 20 } \ln 2$ 
C)  $e ^ { - ( 20 / 57 ) \ln 2 }$ 
D)  $\frac { 20 } { 57 } \ln 2$ 
E)  $e ^ { ( 57 / 20 ) \ln 2 }$ 
F) $\frac { 1 } { 57 } \ln 20$ 
G) $e ^ { ( 20 / 57 ) \ln 2 }$ 
H) $\frac { 1 } { 20 } \ln 57$ 
A)  $e ^ { - ( 57 / 20 ) \ln 2 }$ 
B)  $\frac { 57 } { 20 } \ln 2$ 
C)  $e ^ { - ( 20 / 57 ) \ln 2 }$ 
D)  $\frac { 20 } { 57 } \ln 2$ 
E)  $e ^ { ( 57 / 20 ) \ln 2 }$ 
F) $\frac { 1 } { 57 } \ln 20$ 
G) $e ^ { ( 20 / 57 ) \ln 2 }$ 
H) $\frac { 1 } { 20 } \ln 57$

Question 11

Consider the differential equation $\frac { d y } { d x } = 2 x + y$ .(a) Sketch the direction field. Indicate where the slopes are $- 1$ , 0, or 1. Draw some other slopes as well.(b) If the point $( 1,2 )$ is on the graph of a solution, use Euler's Method with step size $0.5$ to estimate the value of the solution at $x = 2.5$ .

Accepted Answer

The answer of Consider the differential equation \(\frac { d...

Question 12

In a certain medical treatment, a tracer dye is injected into a human organ to measure its function rate and the rate of change of the amount of dye is proportional to the amount present at any time. If a physician injects 0.5 g of dye and 30 minutes later 0.1 g remains, how much dye will be present in $1 \frac { 1 } { 2 }$ hours?

Accepted Answer

The answer of In a certain medical treatment, a tracer...

Question 13

An object cools at a rate (in ${ } ^ { \circ } \mathrm { C } / \mathrm { min }$ ) equal to $\frac { 1 } { 10 }$ of the difference between its temperature and that of the surrounding air. If a room is kept at 20 $^\circ$ C and the temperature of the object is 28 $^\circ$ C, what is the temperature of the object 5 minutes later?

Accepted Answer

A) 22 
B) 24 
C)  $20 + 5 e ^ { - 1 / 10 }$ 
D)  $20 + 8 e ^ { - 1 / 2 }$ 
E)  $20 + 5 e ^ { - 4 / 5 }$ 
F) $20 + 8 e ^ { - 1 / 10 }$ 
G) $28 - 8 e ^ { - 1 / 10 }$
H) $28 - 10 e ^ { - 1 / 2 }$ 
A) 22 
B) 24 
C)  $20 + 5 e ^ { - 1 / 10 }$ 
D)  $20 + 8 e ^ { - 1 / 2 }$ 
E)  $20 + 5 e ^ { - 4 / 5 }$ 
F) $20 + 8 e ^ { - 1 / 10 }$ 
G) $28 - 8 e ^ { - 1 / 10 }$
H) $28 - 10 e ^ { - 1 / 2 }$

Question 14

Assume the half-life of carbon 14 is 5700 years. A wooden statue is measured with 70% of the carbon-14. How old is the statue?

Accepted Answer

About 2933

Question 15

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y = 0$

Accepted Answer

A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$ 
A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$

Question 16

Which of the following is a solution of the differential equation $\frac { d y } { d x } - 4 x y = 0$

Accepted Answer

A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$ 
A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$

Question 17

A direction field for a differential equation is given below:   
(a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ .
(b) Determine whether the differential equation is autonomous. Explain your answer.

Accepted Answer

(a) @#IMG-DLM& 
(b) It is not

Question 18

A direction field is given below. Which of the following represents its differential equation?

Accepted Answer

A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$ 
A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$

Question 19

Find the solution of the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ .

Accepted Answer

A)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 3 C$ 
B)  $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 3 C }$ 
C)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 9$ 
D)  $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 9 }$ 
E)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 27$ 
F) $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 27 }$ 
G) $y = 3 \ln \left( 1 + t ^ { 2 } \right)$ 
H) $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) }$ 
A)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 3 C$ 
B)  $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 3 C }$ 
C)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 9$ 
D)  $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 9 }$ 
E)  $y = 3 \ln \left( 1 + t ^ { 2 } \right) + 27$ 
F) $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) + 27 }$ 
G) $y = 3 \ln \left( 1 + t ^ { 2 } \right)$ 
H) $y = \sqrt [ 3 ] { 3 \ln \left( 1 + t ^ { 2 } \right) }$

Question 20

A direction field for a differential equation is given below. Use a straightedge to draw the graphs of the Euler approximations to the solution curve over the interval $[ 0,4 ]$ that passes through $y ( 0 ) = 1$ . Use as step sizes $h = 4$ , $h = 2$ , $h = 1$ and $h = 0.5$ .

Accepted Answer

The answer of A direction field for a differential equation...

Which of the following is a solution of the differential equation $\frac { d ^ { 2 } y } { d x ^ { 2 } } + 4 y = 0$

When a child was born, her grandparents placed $1000 in a savings account at 10% interest compounded continuously, to be withdrawn at age 20 to help pay for college. How much money is in the account at the time of withdrawal?

Find the solution to the differential equation $\frac { d y } { d x } = e ^ { x - y }$ that satisfies the initial condition $y ( 0 ) = 1$ .

$2000 is invested at 5% annual interest. Find the value of A(t) at the end of t years if: (a) the interest compounds monthly.(b) the interest compounds continuously.

Which of the following equations is satisfied by the function $x = e ^ { 2 t ^ { 2 } }$ ?

The half-life of Carbon 14 is 5700 years. A wooden table is measured with 80% of Carbon 14 compared with newly cut tree. Find the age of the table.

Carbon 14, with a half-life of 5700 years, is used to estimate the age of organic materials. What fraction of the original amount of carbon 14 would an object have if it were 2000 years old?

Assume the half-life of carbon 14 is 5700 years. A wooden statue is measured with 70% of the carbon-14. How old is the statue?

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y = 0$

Which of the following is a solution of the differential equation $\frac { d y } { d x } - 4 x y = 0$

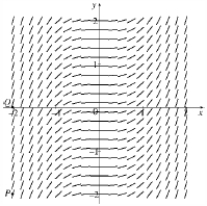A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

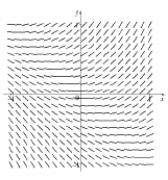
A direction field is given below. Which of the following represents its differential equation?

Find the solution of the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ .

A direction field for a differential equation is given below. Use a straightedge to draw the graphs of the Euler approximations to the solution curve over the interval $[ 0,4 ]$ that passes through $y ( 0 ) = 1$ . Use as step sizes $h = 4$ , $h = 2$ , $h = 1$ and $h = 0.5$ .

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

Exam 7: Differential Equations

Which of the following is a solution of the differential equation d2ydx2+4y=0\frac { d ^ { 2 } y } { d x ^ { 2 } } + 4 y = 0dx2d2y​+4y=0

When a child was born, her grandparents placed $1000 in a savings account at 10% interest compounded continuously, to be withdrawn at age 20 to help pay for college. How much money is in the account at the time of withdrawal?

Find the solution to the differential equation dydx=ex−y\frac { d y } { d x } = e ^ { x - y }dxdy​=ex−y that satisfies the initial condition y(0)=1y ( 0 ) = 1y(0)=1 .

$2000 is invested at 5% annual interest. Find the value of A(t) at the end of t years if: (a) the interest compounds monthly.(b) the interest compounds continuously.

Which of the following equations is satisfied by the function x=e2t2x = e ^ { 2 t ^ { 2 } }x=e2t2 ?

The half-life of Carbon 14 is 5700 years. A wooden table is measured with 80% of Carbon 14 compared with newly cut tree. Find the age of the table.

Carbon 14, with a half-life of 5700 years, is used to estimate the age of organic materials. What fraction of the original amount of carbon 14 would an object have if it were 2000 years old?

Assume the half-life of carbon 14 is 5700 years. A wooden statue is measured with 70% of the carbon-14. How old is the statue?

Which of the following is a solution of the differential equation dydx+4y=0\frac { d y } { d x } + 4 y = 0dxdy​+4y=0

Which of the following is a solution of the differential equation dydx−4xy=0\frac { d y } { d x } - 4 x y = 0dxdy​−4xy=0

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition PPP and initial condition QQQ . (b) Determine whether the differential equation is autonomous. Explain your answer.

A direction field is given below. Which of the following represents its differential equation?

Find the solution of the initial-value problem dydt=2ty2+t2y2\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }dtdy​=y2+t2y22t​ , y(0)=3y ( 0 ) = 3y(0)=3 .

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

Which of the following is a solution of the differential equation $\frac { d ^ { 2 } y } { d x ^ { 2 } } + 4 y = 0$

Find the solution to the differential equation $\frac { d y } { d x } = e ^ { x - y }$ that satisfies the initial condition $y ( 0 ) = 1$ .

Which of the following equations is satisfied by the function $x = e ^ { 2 t ^ { 2 } }$ ?

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y = 0$

Which of the following is a solution of the differential equation $\frac { d y } { d x } - 4 x y = 0$

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Find the solution of the initial-value problem $\frac { d y } { d t } = \frac { 2 t } { y ^ { 2 } + t ^ { 2 } y ^ { 2 } }$ , $y ( 0 ) = 3$ .