Question 1

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ .

Accepted Answer

A)  $y = - \frac { 1 } { 1 - 3 t - t ^ { 2 } }$ 
B)  $y = \frac { 1 } { 1 - 3 t + t ^ { 2 } }$ 
C)  $y = \frac { 1 } { 1 + 3 t - t ^ { 2 } }$ 
D)  $y = \frac { 1 } { 1 - 3 t - t ^ { 2 } }$ 
E)  $y = 1 + 3 t - t ^ { 2 }$ 
F) $y = 1 - 3 y - t ^ { 2 }$
G) $y = 1 - 3 t + t ^ { 2 }$ 
H) $y = - 1 + 3 t + t ^ { 2 }$ 
A)  $y = - \frac { 1 } { 1 - 3 t - t ^ { 2 } }$ 
B)  $y = \frac { 1 } { 1 - 3 t + t ^ { 2 } }$ 
C)  $y = \frac { 1 } { 1 + 3 t - t ^ { 2 } }$ 
D)  $y = \frac { 1 } { 1 - 3 t - t ^ { 2 } }$ 
E)  $y = 1 + 3 t - t ^ { 2 }$ 
F) $y = 1 - 3 y - t ^ { 2 }$
G) $y = 1 - 3 t + t ^ { 2 }$ 
H) $y = - 1 + 3 t + t ^ { 2 }$

Question 2

Suppose $\frac { d y } { d x } = y - x ^ { 2 }$ , $y ( 0 ) = 3$ . Use Euler's method with step size $h = 0.2$ to approximate $y ( 0.4 )$ .

Accepted Answer

A) 3.6 
B) 3.2 
C) 3.4 
D) 5.14 
E) 1
F)4.312
G)4
H)6.1 
A) 3.6 
B) 3.2 
C) 3.4 
D) 5.14 
E) 1
F)4.312
G)4
H)6.1

Question 3

Suppose that a population, P, grows at a rate given by the equation $\frac { d P } { d t } = b P e ^ { - k t }$ , where P is the population (in thousands) at time t (in hours), and b and k are positive constants.(a) Find the solution to the differential equation when b = 0.04, k = 0.01 and P (0) = 1.(b) Find P (10), P (100), and P (1000).(c) After how many hours does the population reach 2 thousand? 30 thousand? 54 thousand?
(d) As time t increases without bound, what happens to the population?
(e) Sketch the graph of the solution of the differential equation.

Accepted Answer

(a) @#IMG-DLM& (b) @#IMG-DLM& (c) The population will reach

Question 4

A direction field is given below. Which of the following represents its differential equation?

Accepted Answer

A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$ 
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$ 
A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$ 
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$

Question 5

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ . What is the carrying capacity?

Accepted Answer

A) 90 
B) 10 
C) 50 
D) 1000 
E) 100
F)60
G)20
H)10,000 
A) 90 
B) 10 
C) 50 
D) 1000 
E) 100
F)60
G)20
H)10,000

Question 6

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y ^ { 2 } = 0$

Accepted Answer

A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$ 
A)  $y = e ^ { - 4 x }$ 
B)  $y = 4 x$ 
C)  $y = e ^ { 2 x ^ { 2 } }$ 
D)  $y = \sin 2 x$ 
E)  $y = e ^ { 2 x }$ 
F) $y = 2 x ^ { 2 }$ 
G) $y = \frac { 1 } { 4 x + 1 }$ 
H) $y = e ^ { 4 x }$

Question 7

According to Newton's Law of Cooling, the temperature $T$ of a warm object decreases at a rate proportional to the difference between $T$ and the temperature $T _ { o }$ of its surroundings.(a) Write down this law as a differential equation.(b) Assume the room temperature is 70 $^\circ$ F. If it takes 2 minutes for a cup of hot coffee to cool down to 180 $^\circ$ F, and how long it takes to cool a cup of coffee from 200 $^\circ$ F to 100 $^\circ$ F.

Accepted Answer

(a) @#IMG-DLM& (b) @#IMG-DLM&

Question 8

The following table contains population data for a Minnesota county for the decades from 1900 to 1980: $$\begin{array} { | l | c | c | c | } 
\hline \text { Year } & \text { Clay County Population } & \begin{array} { c } 
\text { Population Estimate } \
\text { (Exponential Model) }
\end{array} & \begin{array} { c } 
\text { Population Estimate } \
\text { (Logistic Model) }
\end{array} \
\hline 1900 & 17,942 & & \
\hline 1910 & 19,640 & & \
\hline 1920 & 21,780 & & \
\hline 1930 & 23,120 & & \
\hline 1940 & 25,337 & & \
\hline 1950 & 30,363 & & \
\hline 1960 & 39,080 & & \
\hline 1970 & 46,585 & & \
\hline 1980 & 49,327 & & \
\hline
\end{array}$$ (a) Produce a scatter plot for the data.(b) Find an exponential model using the data from 1900 through 1950.(c) Find a logistic model using the data from 1900 through 1950. (Assume the carrying capacity is 440,000.)
(d) Use your models to estimate the population for 1960, 1970, and 1980. Enter your data in the table provided above.

Accepted Answer

(a) @#IMG-DLM& (b) @#IMG-DLM& (Answers may vary.)
(c) @#IMG-DLM& , whe

Question 9

Assume that a population grows at a rate summarized by the equation $\frac { d P } { d t } = \frac { b k P e ^ { - k t } } { 1 - b e ^ { - k t } }$ , where b and k are positive constants (b > 1), and P is the population at time t. Show that $P = \frac { P _ { o } } { 1 - b } \left( 1 - b e ^ { - k t } \right)$ is the general solution for the differential equation (where $P _ { o }$ is the initial population). [Note: This is known as the monomolecular growth curve.]

Accepted Answer

Either solve the equation or s

Question 10

The discharge value on a 1000 liter tank that is filled with water is opened at time t = 0 and the water flows out at a rate of 10 liters per second. At the same time a 1% chlorine mixture enters the tank at a rate of 6 liters per second. Assuming that the solution is well-mixed throughout the tank, what is the concentration of chlorine when the tank is half full?

Accepted Answer

The answer of The discharge value on a 1000 liter...

Question 11

$2000 is invested at 3% annual interest. Find the value of A(t) at the end of t years if:
(a) the interest compounds annually.(b) the interest compounds continuously.

Accepted Answer

The answer of $2000 is invested at 3% annual interest....

Question 12

A direction field for a differential equation is given below: 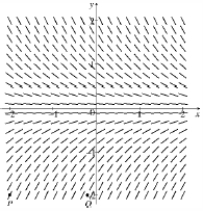  (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ .
(b) Determine whether the differential equation is autonomous. Explain your answer.

Accepted Answer

(a) @#IMG-DLM& 
(b) It is auto

Question 13

$2000 is invested at 5% annual interest. Find the value at the end of 18 years if:
(a) the interest compounds monthly.(b) the interest compounds continuously.

Accepted Answer

(a) About

Question 14

In an experiment, a tissue culture has been subjected to ionizing radiation. It was found that the number A of undamaged cells depends on the exposure time, in hours, according to the formula $A = A _ { 0 } e ^ { k t } , t \geq 0$ If 5000 cells were present initially and 3000 survived a 2-hour exposure, and the elapsed time of exposure after which only half the original cells survive.

Accepted Answer

The answer of In an experiment, a tissue culture has...

Question 15

(a) What can you conclude about the graph of the solution of the equation $\frac { d y } { d x } = - \frac { x } { y }$ just by looking at the differential equation?
(b) Use implicit differentiation to verify all members of the family $x ^ { 2 } + y ^ { 2 } = c ^ { 2 }$ are solutions of the equation in part (a).(c) Find a solution of the equation in part (a) with the additional condition that $y ( 3 ) = 4$ .

Accepted Answer

(a) Let @#IMG-DLM& be a graph of a solut

Question 16

A rumor tends to spread according to the logistic differential equation $\frac { d y } { d t } = 0.3 y - 0.0001 y ^ { 2 }$ , where y is the number of people in the community who have heard the rumor and t is the time in days.(a) Describe the population for this sociological study.(b) Assume that there were 10 people who knew the rumor at initial time t = 0. Find the solution for the differential equation.(c) How many days will it take for half of the population to hear the rumor?

Accepted Answer

(a) @#IMG-DLM& where @#IMG-DLM& is the p

Question 17

Suppose that we model populations of aphids and ladybugs with the system of differential equations: $\begin{array} { l } 
\frac { d A } { d t } = 3 A - 0.01 A L \
\frac { d L } { d t } = - 0.5 L + 0.0001 A L
\end{array}$ Find the expression for $\frac { d A } { d L }$ .

Accepted Answer

A)  $\frac { - 0.5 L + 0.0001 A L } { 3 A - 0.01 A L }$ 
B)  $\frac { 0.5 L - 0.0001 A L } { 3 A - 0.01 A L }$ 
C)  $\frac { - 3 A + 0.01 A L } { - 0.5 + 0.0001 A L }$ 
D)  $\frac { 3 A - 0.01 A L } { - 0.5 L + 0.0001 A L }$ 
E)  $\frac { - 0.5 L + 0.0001 A L } { - 3 A + 0.01 A L }$ 
F) $\frac { - 0.5 L + 0.0001 A L } { - 3 A - 0.01 A L }$ 
G) $\frac { 3 A - 0.01 A L } { 0.5 L - 0.0001 A L }$ 
H) $\frac { 3 A - 0.01 A L } { - 0.5 L - 0.0001 A L }$ 
A)  $\frac { - 0.5 L + 0.0001 A L } { 3 A - 0.01 A L }$ 
B)  $\frac { 0.5 L - 0.0001 A L } { 3 A - 0.01 A L }$ 
C)  $\frac { - 3 A + 0.01 A L } { - 0.5 + 0.0001 A L }$ 
D)  $\frac { 3 A - 0.01 A L } { - 0.5 L + 0.0001 A L }$ 
E)  $\frac { - 0.5 L + 0.0001 A L } { - 3 A + 0.01 A L }$ 
F) $\frac { - 0.5 L + 0.0001 A L } { - 3 A - 0.01 A L }$ 
G) $\frac { 3 A - 0.01 A L } { 0.5 L - 0.0001 A L }$ 
H) $\frac { 3 A - 0.01 A L } { - 0.5 L - 0.0001 A L }$

Question 18

Suppose $\frac { d y } { d x } = y ^ { 2 } - 3$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

Accepted Answer

A) 1 
B) 8 
C) 16 
D) 9 
E) 4
F)14
G)12
H)6 
A) 1 
B) 8 
C) 16 
D) 9 
E) 4
F)14
G)12
H)6

Question 19

A tank contains 500 liters of brine with 10 kg of dissolved salt. Pure water enters the tank at a rate of 10 liters per minute. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank:
(a) after $t$ minutes?
(b) after 10 minutes?

Accepted Answer

The answer of A tank contains 500 liters of brine...

Question 20

A direction field is given below. Which of the following represents its differential equation?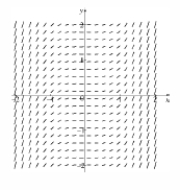

Accepted Answer

A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$ 
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$ 
A)  $\frac { d y } { d x } = \sin x$ 
B)  $\frac { d y } { d x } = - y$ 
C)  $\frac { d y } { d x } = y - \frac { 1 } { 2 } y ^ { 2 }$ 
D)  $\frac { d y } { d x } = x + y$ 
E)  $\frac { d y } { d x } = x ^ { 2 }$ 
F) $\frac { d y } { d x } = 1$ 
G) $\frac { d y } { d x } = y ^ { 2 }$ 
H) $\frac { d y } { d x } = x ^ { 2 } + y ^ { 2 }$

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ .

Suppose $\frac { d y } { d x } = y - x ^ { 2 }$ , $y ( 0 ) = 3$ . Use Euler's method with step size $h = 0.2$ to approximate $y ( 0.4 )$ .

A direction field is given below. Which of the following represents its differential equation?

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ . What is the carrying capacity?

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y ^ { 2 } = 0$

$2000 is invested at 3% annual interest. Find the value of A(t) at the end of t years if: (a) the interest compounds annually.(b) the interest compounds continuously.

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

$2000 is invested at 5% annual interest. Find the value at the end of 18 years if: (a) the interest compounds monthly.(b) the interest compounds continuously.

Suppose that we model populations of aphids and ladybugs with the system of differential equations: =3A-0.01AL =-0.5L+0.0001AL Find the expression for $\frac { d A } { d L }$ .

Suppose $\frac { d y } { d x } = y ^ { 2 } - 3$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

A tank contains 500 liters of brine with 10 kg of dissolved salt. Pure water enters the tank at a rate of 10 liters per minute. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank: (a) after $t$ minutes? (b) after 10 minutes?

A direction field is given below. Which of the following represents its differential equation?

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

Exam 7: Differential Equations

Find the solution of the initial-value problem dydt=2ty2+3y2\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }dtdy​=2ty2+3y2 , y(0)=1y ( 0 ) = 1y(0)=1 .

Suppose dydx=y−x2\frac { d y } { d x } = y - x ^ { 2 }dxdy​=y−x2 , y(0)=3y ( 0 ) = 3y(0)=3 . Use Euler's method with step size h=0.2h = 0.2h=0.2 to approximate y(0.4)y ( 0.4 )y(0.4) .

A direction field is given below. Which of the following represents its differential equation?

Suppose a population growth is modeled by the logistic equation dPdt=0.01P−0.0001P2\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }dtdP​=0.01P−0.0001P2 . What is the carrying capacity?

Which of the following is a solution of the differential equation dydx+4y2=0\frac { d y } { d x } + 4 y ^ { 2 } = 0dxdy​+4y2=0

$2000 is invested at 3% annual interest. Find the value of A(t) at the end of t years if: (a) the interest compounds annually.(b) the interest compounds continuously.

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition PPP and initial condition QQQ . (b) Determine whether the differential equation is autonomous. Explain your answer.

$2000 is invested at 5% annual interest. Find the value at the end of 18 years if: (a) the interest compounds monthly.(b) the interest compounds continuously.

Suppose that we model populations of aphids and ladybugs with the system of differential equations: =3A-0.01AL =-0.5L+0.0001AL Find the expression for dAdL\frac { d A } { d L }dLdA​ .

Suppose dydx=y2−3\frac { d y } { d x } = y ^ { 2 } - 3dxdy​=y2−3 , y(1)=2y ( 1 ) = 2y(1)=2 . Use Euler's method with step size h=1h = 1h=1 to approximate y(3)y ( 3 )y(3) .

A tank contains 500 liters of brine with 10 kg of dissolved salt. Pure water enters the tank at a rate of 10 liters per minute. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank: (a) after ttt minutes? (b) after 10 minutes?

A direction field is given below. Which of the following represents its differential equation?

Functions and Models

Limits and Derivatives

Differentiation Rules

Applications of Differentiation

Integrals

Applications of Integration

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Filters

Find the solution of the initial-value problem $\frac { d y } { d t } = 2 t y ^ { 2 } + 3 y ^ { 2 }$ , $y ( 0 ) = 1$ .

Suppose $\frac { d y } { d x } = y - x ^ { 2 }$ , $y ( 0 ) = 3$ . Use Euler's method with step size $h = 0.2$ to approximate $y ( 0.4 )$ .

Suppose a population growth is modeled by the logistic equation $\frac { d P } { d t } = 0.01 P - 0.0001 P ^ { 2 }$ . What is the carrying capacity?

Which of the following is a solution of the differential equation $\frac { d y } { d x } + 4 y ^ { 2 } = 0$

A direction field for a differential equation is given below: (a) Sketch the graphs of the solutions that have initial condition $P$ and initial condition $Q$ . (b) Determine whether the differential equation is autonomous. Explain your answer.

Suppose that we model populations of aphids and ladybugs with the system of differential equations: =3A-0.01AL =-0.5L+0.0001AL Find the expression for $\frac { d A } { d L }$ .

Suppose $\frac { d y } { d x } = y ^ { 2 } - 3$ , $y ( 1 ) = 2$ . Use Euler's method with step size $h = 1$ to approximate $y ( 3 )$ .

A tank contains 500 liters of brine with 10 kg of dissolved salt. Pure water enters the tank at a rate of 10 liters per minute. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank: (a) after $t$ minutes? (b) after 10 minutes?