Exam 7: Hypothesis Tests and Confidence Intervals in Multiple Regression

If you wanted to test,using a 5% significance level,whether or not a specific slope coefficient is equal to one,then you should

The Solow growth model suggests that countries with identical saving rates and population growth rates should converge to the same per capita income level.This result has been extended to include investment in human capital (education)as well as investment in physical capital.This hypothesis is referred to as the "conditional convergence hypothesis," since the convergence is dependent on countries obtaining the same values in the driving variables.To test the hypothesis,you collect data from the Penn World Tables on the average annual growth rate of GDP per worker (g6090)for the 1960-1990 sample period,and regress it on the (i)initial starting level of GD-P per worker relative to the United States in 1960 (RelProd60), (ii)average population growth rate of the country (n), (iii)average investment share of GDP from 1960 to 1990 (SK - remember investment equals savings),and (iv)educational attainment in years for 1985 (Educ).The results for close to 100 countries is as follows (numbers in parentheses are for heteroskedasticity-robust standard errors): 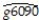= 0.004 - 0.172 × n + 0.133 × SK + 0.002 × Educ - 0.044 × RelProd60, (0.007)(0.209)(0.015)(0.001)(0.008) R2=0.537,SER = 0.011 (a)Is the coefficient on this variable significantly different from zero at the 5% level? At the 1% level? (b)Test for the significance of the other slope coefficients.Should you use a one-sided alternative hypothesis or a two-sided test? Will the decision for one or the other influence the decision about the significance of the parameters? Should you always eliminate variables which carry insignificant coefficients?

To test joint linear hypotheses in the multiple regression model,you need to

Give an intuitive explanation for 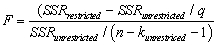.Name conditions under which the F-statistic is large and hence rejects the null hypothesis.

The overall regression F-statistic tests the null hypothesis that

When your multiple regression function includes a single omitted variable regressor,then

When testing joint hypothesis,you should

If the absolute value of your calculated t-statistic exceeds the critical value from the standard normal distribution you can

Females,on average,are shorter and weigh less than males.One of your friends,who is a pre-med student,tells you that in addition,females will weigh less for a given height.To test this hypothesis,you collect height and weight of 29 female and 81 male students at your university.A regression of the weight on a constant,height,and a binary variable,which takes a value of one for females and is zero otherwise,yields the following result: 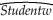= -229.21 - 6.36 × Female + 5.58 × Height,R2=0.50,SER = 20.99 (43.39)(5.74)(0.62) where Studentw is weight measured in pounds and Height is measured in inches (heteroskedasticity-robust standard errors in parentheses). Calculate t-statistics and carry out the hypothesis test that females weigh the same as males,on average,for a given height,using a 10% significance level.What is the alternative hypothesis? What is the p-value? What critical value did you use?

Explain carefully why testing joint hypotheses simultaneously,using the F-statistic,does not necessarily yield the same conclusion as testing them sequentially ("one at a time" method),using a series of t-statistics.

For a single restriction (q = 1),the F-statistic

All of the following are true,with the exception of one condition:

When there are two coefficients,the resulting confidence sets are

The administration of your university/college is thinking about implementing a policy of coed floors only in dormitories.Currently there are only single gender floors.One reason behind such a policy might be to generate an atmosphere of better "understanding" between the sexes.The Dean of Students (DoS)has decided to investigate if such a behavior results in more "togetherness" by attempting to find the determinants of the gender composition at the dinner table in your main dining hall,and in that of a neighboring university,which only allows for coed floors in their dorms.The survey includes 176 students,63 from your university/college,and 113 from a neighboring institution. The Dean's first problem is how to define gender composition.To begin with,the survey excludes single persons' tables,since the study is to focus on group behavior.The Dean also eliminates sports teams from the analysis,since a large number of single-gender students will sit at the same table.Finally,the Dean decides to only analyze tables with three or more students,since she worries about "couples" distorting the results.The Dean finally settles for the following specification of the dependent variable: GenderComp = Where " 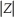" stands for absolute value of Z.The variable can take on values from zero to fifty. After considering various explanatory variables,the Dean settles for an initial list of eight,and estimates the following relationship,using heteroskedasticity-robust standard errors (this Dean obviously has taken an econometrics course earlier in her career and/or has an able research assistant): = 30.90 - 3.78 × Size - 8.81 × DCoed + 2.28 × DFemme +2.06 × DRoommate (7.73)(0.63)(2.66)(2.42)(2.39) - 0.17 × DAthlete + 1.49 × DCons - 0.81 SAT + 1.74 × SibOther,R2=0.24,SER = 15.50 (3.23)(1.10)(1.20)(1.43) where Size is the number of persons at the table minus 3;DCoed is a binary variable,which takes on the value of 1 if you live on a coed floor;DFemme is a binary variable,which is 1 for females and zero otherwise;DRoommate is a binary variable which equals 1 if the person at the table has a roommate and is zero otherwise;DAthlete is a binary variable which is 1 if the person at the table is a member of an athletic varsity team;DCons is a variable which measures the political tendency of the person at the table on a seven-point scale,ranging from 1 being "liberal" to 7 being "conservative";SAT is the SAT score of the person at the table measured on a seven-point scale,ranging from 1 for the category "900-1000" to 7 for the category "1510 and above";and increasing by one for 100 point increases;and SibOther is the number of siblings from the opposite gender in the family the person at the table grew up with. (a)Indicate which of the coefficients are statistically significant. (b)Based on the above results,the Dean decides to specify a more parsimonious form by eliminating the least significant variables.Using the F-statistic for the null hypothesis that there is no relationship between the gender composition at the table and DFemme,DRoommate,DAthlete,and SAT,the regression package returns a value of 1.10.What are the degrees of freedom for the statistic? Look up the 1% and 5% critical values from the F- table and make a decision about the exclusion of these variables based on the critical values. (c)The Dean decides to estimate the following specification next: = 29.07 - 3.80 × Size - 9.75 × DCoed + 1.50 × DCons + 1.97 × SibOther, (3.75)(0.62)(1.04)(1.04)(1.44) R2=0.22 SER = 15.44 Calculate the t-statistics for the coefficients and discuss whether or not the Dean should attempt to simplify the specification further.Based on the results,what might some of the comments be that she will write up for the other senior administrators of your college? What are some of the potential flaws in her analysis? What other variables do you think she should have considered as explanatory factors?

Consider the following Cobb-Douglas production function Yi = AK 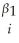L 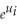(where Y is output,A is the level of technology,K is the capital stock,and L is the labor force),which has been linearized here (by using logarithms)to look as follows: yi = 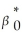+ β1ki + β2li + ui Assuming that the errors are heteroskedastic,you want to test for constant returns to scale.Using a t-statistic and "Approach #2," how would you proceed.

The homoskedasticity-only F-statistic and the heteroskedasticity-robust F-statistic typically are

The homoskedasticity-only F-statistic is given by the following formula

A subsample from the Current Population Survey is taken,on weekly earnings of individuals,their age,and their gender.You have read in the news that women make 70 cents to the $1 that men earn.To test this hypothesis,you first regress earnings on a constant and a binary variable,which takes on a value of 1 for females and is 0 otherwise.The results were: 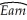= 570.70 - 170.72 × Female,R2=0.084,SER = 282.12. (9.44)(13.52) (a)Perform a difference in means test and indicate whether or not the difference in the mean salaries is significantly different.Justify your choice of a one-sided or two-sided alternative test.Are these results evidence enough to argue that there is discrimination against females? Why or why not? Is it likely that the errors are normally distributed in this case? If not,does that present a problem to your test? (b)Test for the significance of the age and gender coefficients.Why do you think that age plays a role in earnings determination?

You have estimated the relationship between testscores and the student-teacher ratio under the assumption of homoskedasticity of the error terms.The regression output is as follows: = 698.9 - 2.28 × STR,and the standard error on the slope is 0.48.The homoskedasticity-only "overall" regression F- statistic for the hypothesis that the Regression R2 is zero is approximately

The general answer to the question of choosing the scale of the variables is