Exam 18: The Theory of Multiple Regression
Exam 1: Economic Questions and Data17 Questions
Exam 2: Review of Probability71 Questions
Exam 3: Review of Statistics63 Questions
Exam 4: Linear Regression With One Regressor65 Questions
Exam 5: Regression With a Single Regressor: Hypothesis Tests and Confidence Intervals59 Questions
Exam 6: Linear Regression With Multiple Regressors65 Questions
Exam 7: Hypothesis Tests and Confidence Intervals in Multiple Regression65 Questions
Exam 8: Nonlinear Regression Functions62 Questions
Exam 9: Assessing Studies Based on Multiple Regression65 Questions
Exam 10: Regression With Panel Data50 Questions
Exam 11: Regression With a Binary Dependent Variable50 Questions
Exam 12: Instrumental Variables Regression50 Questions
Exam 13: Experiments and Quasi-Experiments50 Questions
Exam 14: Introduction to Time Series Regression and Forecasting50 Questions
Exam 15: Estimation of Dynamic Causal Effects50 Questions
Exam 16: Additional Topics in Time Series Regression50 Questions
Exam 17: The Theory of Linear Regression With One Regressor49 Questions
Exam 18: The Theory of Multiple Regression50 Questions
Select questions type
You have obtained data on test scores and student-teacher ratios in region A and region B of your state.Region B,on average,has lower student-teacher ratios than region A.You decide to run the following regression.
Yi = β0+ β1X1i + β2X2i + β3X3i+ui
where X1 is the class size in region A,X2 is the difference between the class size between region A and B,and X3 is the class size in region B.Your regression package shows a message indicating that it cannot estimate the above equation.What is the problem here and how can it be fixed? Explain the problem in terms of the rank of the X matrix.
(Essay)
4.9/5  (36)
(36)
The extended least squares assumptions in the multiple regression model include four assumptions from Chapter 6 (ui has conditional mean zero; (Xi,Yi),i = 1,…,n are i.i.d.draws from their joint distribution;Xi and ui have nonzero finite fourth moments;there is no perfect multicollinearity).In addition,there are two further assumptions,one of which is
(Multiple Choice)
4.8/5  (42)
(42)
Define the GLS estimator and discuss its properties when Ω is known.Why is this estimator sometimes called infeasible GLS? What happens when Ω is unknown? What would the Ω matrix look like for the case of independent sampling with heteroskedastic errors,where var(ui  Xi)= ch(Xi)= σ2
Xi)= ch(Xi)= σ2 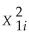 ? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into
? Since the inverse of the error variance-covariance matrix is needed to compute the GLS estimator,find Ω-1.The textbook shows that the original model Y = Xβ + U will be transformed into 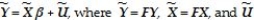 = FU,and
= FU,and  F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data.
F = Ω-1.Find F in the above case,and describe what effect the transformation has on the original data.
(Essay)
4.8/5  (34)
(34)
Your textbook derives the OLS estimator as  =
= 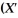 X)-1
X)-1  Y.
Show that the estimator does not exist if there are fewer observations than the number of explanatory variables,including the constant.What is the rank of
Y.
Show that the estimator does not exist if there are fewer observations than the number of explanatory variables,including the constant.What is the rank of  X in this case?
X in this case?
(Essay)
4.8/5  (47)
(47)
The OLS estimator for the multiple regression model in matrix form is
(Multiple Choice)
4.9/5  (45)
(45)
The leading example of sampling schemes in econometrics that do not result in independent observations is
(Multiple Choice)
4.9/5  (35)
(35)
The multiple regression model can be written in matrix form as follows:
(Multiple Choice)
4.8/5  (43)
(43)
One implication of the extended least squares assumptions in the multiple regression model is that
(Multiple Choice)
4.8/5  (36)
(36)
Using the model Y = Xβ + U,and the extended least squares assumptions,derive the OLS estimator 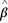 .Discuss the conditions under which
.Discuss the conditions under which 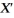 X is invertible.
X is invertible.
(Essay)
5.0/5  (34)
(34)
The linear multiple regression model can be represented in matrix notation as Y= Xβ + U,where X is of order n×(k+1).k represents the number of
(Multiple Choice)
4.7/5  (36)
(36)
Consider the following population regression function: Y = Xβ + U
where Y=  ,X=
,X= 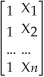 ,β =
,β = 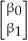 ,U=
,U=  Given the following information on population growth rates (Y)and education (X)for 86 countries
Given the following information on population growth rates (Y)and education (X)for 86 countries  ,
, 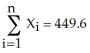 ,
,  ,
, 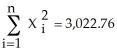 ,
,  a)find X'X,X'Y, (X'X)-1 and finally (X'X)-1 X'Y.
b)Interpret the slope,and if necessary,the intercept.
a)find X'X,X'Y, (X'X)-1 and finally (X'X)-1 X'Y.
b)Interpret the slope,and if necessary,the intercept.
(Essay)
4.8/5  (34)
(34)
Showing 21 - 40 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)