Exam 18: The Theory of Multiple Regression

Assume that the data looks as follows: Y = ,U = ,X = ,and β = (β1) Using the formula for the OLS estimator = ( X)-1 Y,derive the formula for 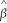1,the only slope in this "regression through the origin."

The difference between the central limit theorems for a scalar and vector-valued random variables is

In the case when the errors are homoskedastic and normally distributed,conditional on X,then

Write an essay on the difference between the OLS estimator and the GLS estimator.

A joint hypothesis that is linear in the coefficients and imposes a number of restrictions can be written as

Let there be q joint hypothesis to be tested.Then the dimension of r in the expression Rβ = r is

In order for a matrix A to have an inverse,its determinant cannot be zero.Derive the determinant of the following matrices: A = B = X'X where X = (1 10)

To prove that the OLS estimator is BLUE requires the following assumption

Give several economic examples of how to test various joint linear hypotheses using matrix notation.Include specifications of Rβ = r where you test for (i)all coefficients other than the constant being zero, (ii)a subset of coefficients being zero,and (iii)equality of coefficients.Talk about the possible distributions involved in finding critical values for your hypotheses.

Consider the following symmetric and idempotent Matrix A: A = I - ιι' and ι = a.Show that by postmultiplying this matrix by the vector Y (the LHS variable of the OLS regression),you convert all observations of Y in deviations from the mean. b.Derive the expression Y'AY.What is the order of this expression? Under what other name have you encountered this expression before?