Exam 13: Introduction to Optimization Modeling
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
A Solver's sensitivity report shows sensitivity to objective coefficients and right sides of constraints.
(True/False)
4.7/5  (38)
(38)
Suppose an objective function has the equation: 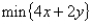 .
Then the slope of the objective function line is 2.
.
Then the slope of the objective function line is 2.
(True/False)
4.9/5  (22)
(22)
When formulating a linear programming spreadsheet model, we specify the constraints in a Solver dialog box, since Excel does not show the constraints directly.
(True/False)
4.8/5  (33)
(33)
Reduced costs indicate how much the objective coefficient of a decision variable that is currently 0 or at its upper bound must change before that the value of that variable changes.
(True/False)
4.9/5  (39)
(39)
Linear programming problems can always be formulated algebraically, but not always on a spreadsheet.
(True/False)
4.8/5  (32)
(32)
If an LP model has an unbounded solution, then we must have made a mistake - either we have made an input error or we omitted one or more constraints.
(True/False)
4.7/5  (34)
(34)
The value, such as profit, to be optimized in an optimization model is the objective.
(True/False)
4.8/5  (32)
(32)
Suppose a firm must at least meet minimum expected demands of 60 for product x and 80 of product y. An algebraic formulation of these constraints is:
(Multiple Choice)
4.8/5  (25)
(25)
It is often useful to perform sensitivity analysis to see how, or if, the optimal solution to a linear programming problem changes as we change one or more model inputs.
(True/False)
4.8/5  (29)
(29)
A company produces two products. Each product can be produced on either of two machines. The time (in hours) required to produce each product on each machine is shown below:  Each month, 600 hours of time are available on each machine, and that customers are willing to buy up to the quantities of each product at the prices that are shown below:
Each month, 600 hours of time are available on each machine, and that customers are willing to buy up to the quantities of each product at the prices that are shown below:  The company's goal is to maximize the revenue obtained from selling units during the next two months.
-What are the constraints in this problem?
The company's goal is to maximize the revenue obtained from selling units during the next two months.
-What are the constraints in this problem?
(Essay)
4.8/5  (47)
(47)
In some cases, a linear programming problem can be formulated such that the objective can become infinitely large (for a maximization problem) or infinitely small (for a minimization problem). This type of problem is said to be:
(Multiple Choice)
4.8/5  (37)
(37)
A chemical manufacturer produces two products, chemical X and chemical Y. Each product is manufactured by a two-step process that involves blending and mixing in machine A and packaging on machine B. Chemical X provides a $60/unit contribution to profit, while Chemical Y provides a $50 contribution to profit. The processing times for the two products on the mixing machine (A) and the packaging machine (B) are as follows: 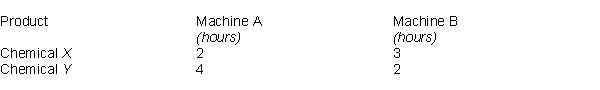 For the upcoming two-week period, machine A has available 80 hours and machine B has available 60 hours of processing time. Forecasts of the markets indicate that the manufacturer can expect to sell a maximum of 16 units of chemical X and 18 units of chemical Y.
-What are the decision variables in this problem?
For the upcoming two-week period, machine A has available 80 hours and machine B has available 60 hours of processing time. Forecasts of the markets indicate that the manufacturer can expect to sell a maximum of 16 units of chemical X and 18 units of chemical Y.
-What are the decision variables in this problem?
(Essay)
4.8/5  (33)
(33)
In general, the complete solution of a linear programming problem involves three stages: formulating the model, invoking Solver to find the optimal solution, and performing sensitivity analysis.
(True/False)
4.8/5  (42)
(42)
There are two primary ways to formulate a linear programming problem: the traditional algebraic way and with spreadsheets.
(True/False)
4.8/5  (33)
(33)
In using Excel® to solve linear programming problems, the decision variable cells represent the:
(Multiple Choice)
4.8/5  (31)
(31)
The solution of a linear programming problem using Excel® typically involves the following three stages:
(Multiple Choice)
4.8/5  (37)
(37)
In using Excel® to solve linear programming problems, the objective cell represents the:
(Multiple Choice)
4.9/5  (37)
(37)
Showing 21 - 40 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)