Exam 13: Introduction to Optimization Modeling
Exam 1: Introduction to Business Analytics29 Questions
Exam 2: Describing the Distribution of a Single Variable100 Questions
Exam 3: Finding Relationships Among Variables85 Questions
Exam 4: Probability and Probability Distributions114 Questions
Exam 5: Normal, Binomial, Poisson, and Exponential Distributions125 Questions
Exam 6: Decision Making Under Uncertainty107 Questions
Exam 7: Sampling and Sampling Distributions90 Questions
Exam 8: Confidence Interval Estimation84 Questions
Exam 9: Hypothesis Testing87 Questions
Exam 10: Regression Analysis: Estimating Relationships92 Questions
Exam 11: Regression Analysis: Statistical Inference82 Questions
Exam 12: Time Series Analysis and Forecasting106 Questions
Exam 13: Introduction to Optimization Modeling97 Questions
Exam 14: Optimization Models114 Questions
Exam 15: Introduction to Simulation Modeling82 Questions
Exam 16: Simulation Models102 Questions
Exam 17: Data Mining20 Questions
Exam 18: Importing Data Into Excel19 Questions
Exam 19: Analysis of Variance and Experimental Design20 Questions
Exam 20: Statistical Process Control20 Questions
Select questions type
All optimization problems include decision variables, an objective function, and constraints.
(True/False)
4.8/5  (41)
(41)
Consider the following linear programming problem: Minimize: 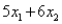 Subject to:
Subject to: 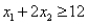
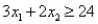
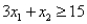
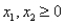 The above linear programming problem:
The above linear programming problem:
(Multiple Choice)
4.9/5  (28)
(28)
The divisibility property of LP models simply means that we allow only integer levels of the activities.
(True/False)
4.8/5  (43)
(43)
A farmer in Egypt owns 50 acres of land. He is going to plant each acre with cotton or corn. Each acre planted with cotton yields $400 profit; each with corn yields $200 profit. The labor and fertilizer used for each acre are given in the table below. Resources available include 150 workers and 200 tons of fertilizer.  -(A) Formulate a linear programming model that will enable the farmer to determine the number of acres that should be planted cotton and/or corn in order to maximize his profit.
(B) Find an optimal solution to the model in (A) and determine the maximum profit.
(C) Implement the model in (A) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution?
(D) Obtain a sensitivity report for the model in (A). How much should the farmer be willing to pay for an additional worker?
(E) Suppose the farmer hires 10 additional workers. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Would his planting plan change? Explain your answer.
(F) Suppose the farmer now wants to hire 20 additional workers, instead of just 10. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Explain your answer.
-(A) Formulate a linear programming model that will enable the farmer to determine the number of acres that should be planted cotton and/or corn in order to maximize his profit.
(B) Find an optimal solution to the model in (A) and determine the maximum profit.
(C) Implement the model in (A) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution?
(D) Obtain a sensitivity report for the model in (A). How much should the farmer be willing to pay for an additional worker?
(E) Suppose the farmer hires 10 additional workers. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Would his planting plan change? Explain your answer.
(F) Suppose the farmer now wants to hire 20 additional workers, instead of just 10. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Explain your answer.
(Essay)
4.9/5  (31)
(31)
As related to sensitivity analysis in linear programming, when the profit increases with a unit increase in labor, this change in profit is referred to as the:
(Multiple Choice)
4.8/5  (31)
(31)
When there is a problem with Solver being able to find a solution, many times it is an indication of a(n):
(Multiple Choice)
4.8/5  (41)
(41)
When the proportionality property of LP models is violated, we generally must use non-linear optimization.
(True/False)
4.8/5  (44)
(44)
Unboundedness refers to the situation in which the LP model has been formulated in such a way that the objective function is unbounded - that is, it can be made as large (for maximization problems) or as small (for minimization problems) as we wish.
(True/False)
4.7/5  (34)
(34)
Nonbinding constraints will always have slack, which is the difference between the two sides of the inequality in the constraint equation.
(True/False)
4.7/5  (34)
(34)
A company produces two products. Each product can be produced on either of two machines. The time (in hours) required to produce each product on each machine is shown below:  Each month, 600 hours of time are available on each machine, and that customers are willing to buy up to the quantities of each product at the prices that are shown below:
Each month, 600 hours of time are available on each machine, and that customers are willing to buy up to the quantities of each product at the prices that are shown below:  The company's goal is to maximize the revenue obtained from selling units during the next two months.
-What is the objective function in this problem?
The company's goal is to maximize the revenue obtained from selling units during the next two months.
-What is the objective function in this problem?
(Essay)
4.8/5  (39)
(39)
Linear programming models have three important properties: _____.
(Multiple Choice)
4.8/5  (27)
(27)
The term nonnegativity refers to the condition in which the:
(Multiple Choice)
4.9/5  (29)
(29)
If a manufacturing process takes 3 hours per unit of x and 5 hours per unit of y and a maximum of 100 hours of manufacturing process time are available, then an algebraic formulation of this constraint is:
(Multiple Choice)
4.9/5  (30)
(30)
In determining the optimal solution to a linear programming problem graphically, if the objective is to maximize the objective, we pull the objective function line down until it contacts the feasible region.
(True/False)
5.0/5  (35)
(35)
It is instructive to look at a graphical solution procedure for LP models with three or more decision variables.
(True/False)
4.8/5  (33)
(33)
The optimal solution to any linear programming model is a corner point of a polygon.
(True/False)
4.8/5  (29)
(29)
A shadow price indicates how much a company would pay for more of a scarce resource.
(True/False)
4.9/5  (30)
(30)
A feasible solution is a solution that satisfies all of the constraints.
(True/False)
4.9/5  (39)
(39)
Showing 61 - 80 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)