Exam 13: Introduction to Optimization Modeling

If a solution to an LP problem satisfies all of the constraints, then it must be feasible.

Suppose the allowable increase and decrease for an objective coefficient of a decision variable that has a current value of $50 are $25 (increase) and $10 (decrease). If the coefficient were to change from $50 to $60, the optimal value of the objective function would not change.

There is often more than one objective in linear programming problems.

The set of all values of the decision variable cells that satisfy all constraints, not including the nonnegativity constraints, is called the feasible region.

When formulating a linear programming spreadsheet model, there is a set of designated cells that play the role of the decision variables. These are called the objective cells.

A company produces two products. Each product can be produced on either of two machines. The time (in hours) required to produce each product on each machine is shown below: Each month, 600 hours of time are available on each machine, and that customers are willing to buy up to the quantities of each product at the prices that are shown below: The company's goal is to maximize the revenue obtained from selling units during the next two months. -What are the decision variables in this problem?

Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant, which produces 5000 tons per month, and the Lakeview plant, which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants: Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: 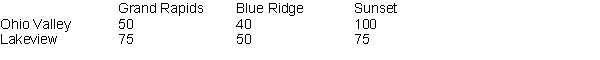-What are the decision variables in this problem?

The divisibility property of linear programming means that a solution can have both:

Conditions that must be satisfied in an optimization model are:​

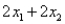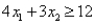
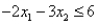
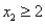
Consider the following linear programming problem: Maximize: Subject to: 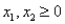The above linear programming problem:

The additivity property of LP models implies that the sum of the contributions from the various activities to a particular constraint equals the total contribution to that constraint.

Infeasibility refers to the situation in which there are no feasible solutions to the LP model.

The additivity property of linear programming implies that the contribution of any decision variable to the objective is of/on the levels of the other decision variables.

The feasible region in a graphical solution of a linear programming problem will appear as some type of polygon, with lines forming all sides.

Binding constraints are constraints that hold as an equality.​

Proportionality, additivity, and divisibility are three important properties that LP models possess that distinguish them from general mathematical programming models.

(A) Verify that Mary should purchase 12 units of food 2 each day and thus oversatisfy the vitamin C requirement by 6 units. ​ (B) Mary's husband has put his foot down and demanded that Mary fulfill the family's daily nutritional requirement exactly by obtaining precisely 12 units of vitamin A and 6 units of vitamin C. The optimal solution to the new problem will involve ingesting less vitamin C, but it will be more expensive, why? ​ (C) Starting with the optimal solution to (B), use the SolverTable add-in to see what happens to the total cost when the vitamin A and vitamin C requirements both vary (independently) from 3 to 18 in 3-unit increments. That is, from a two-way table. Describe the behavior you observe. In particular, are the changes in total cost the same as you look across each row of the table? Are they the same as you look across each column of the table?